№262 (6) , учебник Ю.М. Колягин , Алгебра-10 класс. Доказать , что число ( 71³²⁵ + 41¹³⁵ ) делится на 7.
Максимально ПОДРОБНО, используя теорию только данного учебника.

Пошаговое объяснение:

262 ( 6 ) . Розв"язуємо за до порівнянь ( сравнений ) .

71³²⁵ + 41¹³⁵ ≡ 1 (mod 7) + 6 (mod 7) ≡ 7 (mod 7) ≡ 0 (mod 7) .

Отже , остача від ділення даного числового виразу на 7 дорівнює 0 ,

а це означає , що він ділиться на 7 .  

Пошаговое объяснение:

1) Формула для n-натурального числа

Значит число вида делится на a-b, при условии a-b≠0

2) Формула для n-нечётного числа

Значит число вида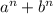 , где n-нечётно, делится на a+b, при условии a+b≠0

3) 71³²⁵-1=71³²⁵-1³²⁵ делится на 71-1=70(по первой формуле). Значит делится и на 7, так как 70 кратно 7.

4) 41¹³⁵+1=41¹³⁵+1¹³⁵ делится на 41+1=42(по 2-ой формуле). Значит делится и на 7, так как 42 кратно 7

5) Получим что число  71³²⁵ + 41¹³⁵=(71³²⁵ -1)+ (41¹³⁵+1)  делится на 7, так как каждое из слагаемых (71³²⁵ -1)  и  (41¹³⁵+1)  делится на 7