25б Найти наибольшее и наименьшее значение функции, на отрезке [-2;-0,5]
дайте подробное решение с рисунками
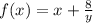
Другие вопросы по теме Математика
Популярные вопросы
- Расскажите о биографии Чичикова по плану: 1) Тяжёлая картина раннего детства;...
1 - До ть з написанням твору на тему родина це вся україна з глибоким корінням...
2 - В «Истории первой, в которой говорится о зеркале его осколках», преобладает...
1 - Найдите число x, чтобы равенство было верным. 1)3,82*x=3,056 2)0,77:x=1,4...
3 - Что не типично для произведений М.М.Пришвина?...
3 - 1. Найдите соответствующую пару глаголов и определите отличия. Запишите видовые...
1 - Здравствуйте Перепишите предложения и вставьте, где нужно артикль «а» 1. You...
1 - Choose the correct options —  Have you spoken Did you speak to Bob yet? —...
2 - Найдите площадь трапеции, изображённой на рисунке....
1 - Объем параллелепипеда равен 64 см/куб, ширина- 4 см, высота- 2 см.Длину этого...
3
↓↓↓
Пошаговое объяснение:
fꞌ(x)= (x+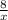 ) ꞌ=1 +
) ꞌ=1 +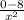 =
= 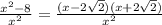 .
.
x=2√2 ∉ [-2;-0,5] , x=-2√2∉ [-2;-0,5]
Наибольшее и наименьшее значение функции достигается либо на концах отрезка либо в точках экстремума.
f(-2)=-2+8\(-2)=-6 наибольшее значение функции
f(-0,5)= -0,5+8\(-0,5)= -16,5 наименьшее значение функции
Решение задания прилагаю