235.
Центр круга (-1; 2), а радиус √10:
а) построить уравнение круга.
б) понять, находятся ли точки
A(-3, 5), B (-2, -1) и C (2, 2) на окружности, внутри окружности или за ее пределами?
​

а) Уравнение окружности с центром в точке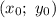 и радиусом 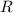имеет вид: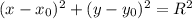

Имеем: центр окружности в точке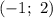 и радиус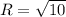

Уравнение окружности: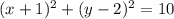

б) Имеем точки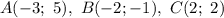

Точка с координатами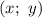 находится на окружности, если 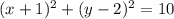, внутри окружности — 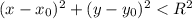, за пределами окружности —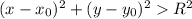

Проверка:

— точка находится за пределами окружности.

— точка находится на окружности.

— точка находится внутри окружности.