2. Запиши координаты точек A, B, C и D. Выпиши точки, которые находятся на одинаковом расстоянии от начала отсчета.
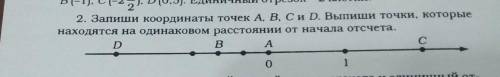
Другие вопросы по теме Математика
Популярные вопросы
- Хорды ав и сd пересекаются в точке к. найдите значение х, если...
2 - Ть будь ласка з хімією а то у мене не дуже вихотить? ( 13 варіант...
1 - Сколько времени у вас занимает интернет ( ответ должен составлять...
1 - Вкакой отрасли начелся промышленный переварот в...
2 - Решить . над озерами летели гуси. на первом озере села половина...
3 - 5мячиков стоят 32 руб. сколько стоят 7 таких мячиков...
1 - 12. отметь ряд, в котором все слова - это имена существительные...
3 - *запишите и решите пример: найдите произведение разности чисел...
2 - Продолжение асыл тастармен әшекейленген желегі бар сәукеле- қыздың...
3 - Определи порядок действий и найди значения выражений 370+12: 4+7...
2
кут D 70° kyt B 160° kyt A 30° C310°
Пошаговое объяснение:
Если не веришь возьми и сам вимиряй
На данной картинке изображена координатная плоскость. Во-первых, давайте запишем координаты точек A, B, C и D.
Точка A у нас находится на пересечении оси x и оси y. Поэтому ее координаты будут (0, 0).
Точка B находится на оси x и на расстоянии 4 единицы от начала отсчета. Так как она находится только на оси x, то у нее вторая координата будет 0. Значит, координаты точки B будут (4, 0).
Точка C находится на оси y и на расстоянии 3 единицы от начала отсчета. Так как она находится только на оси y, то у нее первая координата будет 0. Значит, координаты точки C будут (0, 3).
Точка D находится где-то в третьем квадранте и на расстоянии 5 единицы от начала отсчета. Мы видим, что у точки D отрицательные значения по обеим осям. Поэтому координаты точки D будут (-5, -5).
Теперь мы должны найти точки, которые находятся на одинаковом расстоянии от начала отсчета. Расстояние от начала отсчета до точки можно найти с помощью формулы: расстояние = √(x^2 + y^2), где x и y - это координаты точки.
Давайте найдем расстояние от начала отсчета до точки A:
расстояние(A) = √(0^2 + 0^2) = √(0 + 0) = √0 = 0
Расстояние от начала отсчета до точки B:
расстояние(B) = √(4^2 + 0^2) = √(16 + 0) = √16 = 4
Расстояние от начала отсчета до точки C:
расстояние(C) = √(0^2 + 3^2) = √(0 + 9) = √9 = 3
Расстояние от начала отсчета до точки D:
расстояние(D) = √((-5)^2 + (-5)^2) = √(25 + 25) = √50 ≈ 7.07 (округляем до сотых)
Итак, мы получили следующие расстояния от начала отсчета до точек:
расстояние(A) = 0
расстояние(B) = 4
расстояние(C) = 3
расстояние(D) ≈ 7.07
Теперь остается найти точки, которые находятся на одинаковом расстоянии от начала отсчета. По нашим вычислениям, точки, которые находятся на одинаковом расстоянии от начала отсчета, это точка A и точка D, так как расстояние от начала отсчета до этих точек равно 0.
Надеюсь, я смог объяснить решение задачи понятным образом. Если у вас возникнут еще вопросы, не стесняйтесь задавать!