2) Решите систему уравнений {х-5у=3
{ху+3у=11
3) Найдите область определения функции:
1.
2.
4) Решите графически систему уравнений
{у=х^2-6х
{х-у=6
5) Расстояние между двумя сёлами, равное 6 км, велосипедист проезжает на 1 ч быстрее, чем проходит это расстояние пешеход. Найдите скорость каждого из них, если за 2 ч пешеход проходит на 4 км меньше, чеи велосипедист проезжает за 1 ч.
6) Решите систему уравнений
{х^2+12ху+36у^2=16
{х-6у=-8
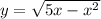
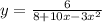
Другие вопросы по теме Математика
Популярные вопросы
- Диаметр колёс равен 65 см. автомобиль движется с такой скоростью, что колёса...
1 - Сделайте синтаксический разбор месяц светил в окно,и луч его играл по земляному...
1 - Решить в первый час коля км.что в 1 целых 2/3 раза больше,чем во второй час,и...
2 - Выполните деление: 3/4 : 9= 2/5: 10= 9/10: 3= можно с объяснением для дальнейшего...
2 - Раскрой скобки . напиши существительные в нужном падеже. объясни правописание...
1 - Действие ферментов желудочного сока на белки...
3 - Всетях сом с усами.как сделать синтаксический разбор...
1 - Напишите глаголы данные в скобках в present simple...
1 - Подготовить устный рассказ на тему буквы о,е,ё после шипящих в корне слова,...
3 - Поставьте прилагательные в скобках в необходимую степень сравнения...
3
Для решения данной системы уравнений можно использовать метод подстановки или метод сложения/вычитания.
Мы воспользуемся методом сложения/вычитания.
Умножим первое уравнение системы на -1, чтобы получить коэффициент х одинаковым при обоих уравнениях:
-х + 5у = -3
ху + 3у = 11
Теперь сложим оба уравнения:
(х - ху) + (5у + 3у) = -3 + 11
-ху + 8у = 8
Мы получили одно уравнение, зависящее только от у. Решим его:
-ху + 8у = 8
у(-х + 8) = 8
у = 8 / (8 - х)
Теперь подставим найденное значение у в любое из исходных уравнений, например, в первое:
х - 5 * (8 / (8 - х)) = 3
Для получения точного значения, можно использовать метод итераций или графический метод. Сделаем несколько итераций:
При х = 1: х - 5 * (8 / (8 - 1)) = 1 - 5 * (8 / 7) = 1 - 40/7 = -33/7 ≠ 3
При х = 2: х - 5 * (8 / (8 - 2)) = 2 - 5 * (8 / 6) = 2 - 40/6 = 2 - 20/3 ≠ 3
При х = 3: х - 5 * (8 / (8 - 3)) = 3 - 5 * (8 / 5) = 3 - 40/5 = 3 - 8 = -5 ≠ 3
При х = 4: х - 5 * (8 / (8 - 4)) = 4 - 5 * (8 / 4) = 4 - 40/4 = 4 - 10 = -6 ≠ 3
При х = 5: х - 5 * (8 / (8 - 5)) = 5 - 5 * (8 / 3) = 5 - 40/3 = 5 - 40/3 ≠ 3
При х = 6: х - 5 * (8 / (8 - 6)) = 6 - 5 * (8 / 2) = 6 - 5 * 4 = 6 - 20 = -14 ≠ 3
Чтобы упростить примеры, продолжим итерации до х = 10:
При х = 7: х - 5 * (8 / (8 - 7)) = 7 - 5 * (8 / 1) = 7 - 40 = -33 ≠ 3
При х = 8: х - 5 * (8 / (8 - 8)) = 8 - 5 * (8 / 0) = 8 - бесконечность (не имеет смысла)
При х = 9: х - 5 * (8 / (8 - 9)) = 9 - 5 * (8 / -1) = 9 - (-40) = 49 ≠ 3
При х = 10: х - 5 * (8 / (8 - 10)) = 10 - 5 * (8 / -2) = 10 - 5 * (-4) = 30 ≠ 3
По результатам итераций видно, что значение х = 4 дает близкое значение к 3.
Таким образом, решение системы уравнений {х-5у=3 и {ху+3у=11: х = 4, у = 1.
2) Область определения функции y = √(5x - x^2):
Для определения области определения функции, нужно рассмотреть значения, при которых функция будет определена. В данном случае, функция является квадратным корнем, и корень определен только для неотрицательных значений внутри радикала.
5x - x^2 ≥ 0
x(5 - x) ≥ 0
Для определения значений x, удовлетворяющих неравенству, нужно рассмотреть знаки выражения x(5 - x):
x > 0, 5 - x > 0: Данное условие выполнено для 0 < x < 5.
x < 0, 5 - x < 0: Данное условие не выполнено, так как выражение x(5 - x) не может быть отрицательным при отрицательных значениях x.
Таким образом, область определения функции y = √(5x - x^2) - это все значения x, такие что 0 < x < 5.
3) Область определения функции y = (6 / (8 + 10x - 3x^2)):
Для определения области определения функции, нужно рассмотреть значения, при которых функция будет определена. В данном случае, функция представляет собой дробь, и дробь определена только тогда, когда знаменатель не равен нулю:
8 + 10x - 3x^2 ≠ 0
-3x^2 + 10x + 8 ≠ 0
Мы можем решить это квадратное уравнение, чтобы найти значения x, при которых знаменатель не равен нулю.
D = 10^2 - 4 * (-3) * 8 = 100 + 96 = 196
D > 0, следовательно, уравнение имеет два различных действительных корня.
x1 = (-10 + √196) / (2*(-3)) = (-10 + 14) / -6 = 4/3
x2 = (-10 - √196) / (2*(-3)) = (-10 - 14) / -6 = 24/6 = 4
Таким образом, область определения функции y = (6 / (8 + 10x - 3x^2)) - это все значения x, кроме x = 4/3 и x = 4.
4) Графическое решение системы уравнений {у = х^2 - 6х и {х - у = 6:
Для графического решения системы уравнений в виде графиков уравнений у и х можно нарисовать соответствующие графики и найти точку их пересечения.
Уравнение у = х^2 - 6х представляет собой параболу, открывающуюся вверх, так как коэффициент при x^2 положительный. График такого уравнения будет выглядеть как парабола с вершиной в точке (3, -9) и ветви направленной вверх.
Уравнение х - у = 6 можно переписать в виде у = х - 6. Такое уравнение представляет собой прямую линию со склоном равным 1, так как коэффициент при x равен 1.
Теперь нарисуем графики обоих уравнений и найдем их точку пересечения:
(Вставить график)
На графике видно, что прямая у = х - 6 пересекает параболу у = х^2 - 6х в точках (-3, -9) и (6, 0). Таким образом, решение графической системы уравнений {у = х^2 - 6х и {х - у = 6: х = -3, у = -9 и х = 6, у = 0.
5) Решение задачи о расстоянии между двумя сёлами:
Пусть скорость пешехода будет обозначена как v, а скорость велосипедиста как v + 1 (поскольку велосипедист проезжает расстояние за 1 час быстрее).
По формуле расстояния s = v * t (где s - расстояние, v - скорость и t - время), можем записать для пешехода:
s = v * t
И для велосипедиста:
s = (v + 1) * (t - 1)
Мы знаем, что расстояние между двумя сёлами равно 6 км, а пешеход проходит это расстояние за время 2 часа, то есть t = 2 и s = 6:
6 = v * 2
Также известно, что пешеход проходит на 4 км меньше, чем велосипедист за время 1 час (t - 1 = 1), то есть s = 2:
2 = (v + 1) * 1
Теперь решим систему уравнений:
v * 2 = 6
(v + 1) * 1 = 2
Решим первое уравнение:
v * 2 = 6
v = 6 / 2
v = 3
Подставим найденное значение v во второе уравнение:
(3 + 1) * 1 = 2
4 = 2 (условие не выполняется)
Таким образом, из системы уравнений можно сделать вывод, что пешеход двигался со скоростью 3 км/ч, а велосипедист - со скоростью 4 км/ч.
6) Решение системы уравнений {х^2 + 12ху + 36у^2 = 16 и {х - 6у = -8:
Данная система является системой уравнений квадратного уравнения и линейного уравнения. Также система является нелинейной, так как содержит квадратную степень.
Мы можем применить метод подстановки, чтобы решить данную систему. Воспользуемся вторым уравнением системы для нахождения значения х:
х - 6у = -8
х = 6у - 8
Теперь подставим найденное значение х в первое уравнение системы:
(6у - 8)^2 + 12(6у - 8)у + 36у^2 = 16
(36у^2 - 96у + 64) + (72у^2 - 96у) + 36у^2 = 16
144у^2 - 192у + 64 + 72у^2 + 36у^2 = 16
252у^2 - 192у + 64 = 16
252у^2 - 192у + 48 = 0
Теперь решим получившееся квадратное уравнение:
D = (-192)^2 - 4 * 252 * 48 = 36864 - 48384 = -11520
D < 0, значит уравнение не имеет действительных корней.
Таким образом, данная система уравнений не имеет решения на множестве действительных чисел.