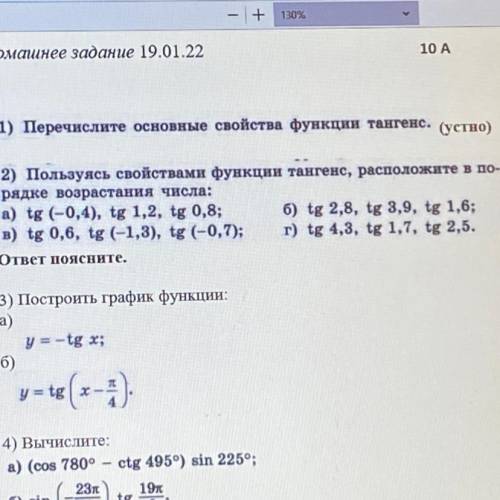
2) Пользуясь свойствами функции тангенс, расположите в по-
рядке возрастания числа:
а) tg (-0,4), tg 1,2, tg 0,8; б) tg 2,8, tg 3,9, tg 1,6;
в) tg 0,6, tg (-1,3), tg (-0,7); г) tg 4,3, tg 1,7, tg 2,5.
ответ поясните.

Для решения данной задачи нам необходимо использовать свойства функции тангенс. Функция тангенс имеет разные значения в различных областях определения.

a) tg (-0,4), tg 1,2, tg 0,8:
-0,4 и 1,2 находятся в первой четверти, где значение тангенса положительно. Таким образом, tg (-0,4) < tg 1,2.
tg 0,8 находится между -1 и 0 на графике тангенса. Таким образом, tg 0,8 < tg (-0,4) < tg 1,2.

б) tg 2,8, tg 3,9, tg 1,6:
2,8, 3,9 и 1,6 находятся во второй четверти, где значение тангенса положительно. Таким образом, tg 2,8 < tg 3,9 < tg 1,6.

в) tg 0,6, tg (-1,3), tg (-0,7):
0,6 находится между 0 и 1 на графике тангенса. Таким образом, tg (-1,3) < tg (-0,7) < tg 0,6.

г) tg 4,3, tg 1,7, tg 2,5:
4,3 находится на границе между третьей и четвертой четвертями, где значение тангенса отрицательно.
1,7 находится между 1 и 2 на графике тангенса. Таким образом, tg 1,7 < tg 2,5.
Также, можно заметить, что tg 4,3 < tg 1,7.

Итак, упорядоченные в порядке возрастания числа:
а) tg (-0,4) < tg 0,8 < tg 1,2
б) tg 2,8 < tg 1,6 < tg 3,9
в) tg (-1,3) < tg (-0,7) < tg 0,6
г) tg 4,3 < tg 1,7 < tg 2,5