2. К плоскости α проведена наклонная AB (A∈α). Длина наклонной равна 20 см, наклонная с плоскостью образует угол 45°. Вычисли, на каком расстоянии от плоскости находится точка B.
Расстояние от точки B до плоскости равно
−−−−−√ см.
(Если в ответе нет корня, то под корнем пиши 1.)
3. В правильной треугольной пирамиде боковое ребро с плоскостью основания образует угол 45°. Высота пирамиды равна 2 см.
Вычисли сторону основания пирамиды.
4.
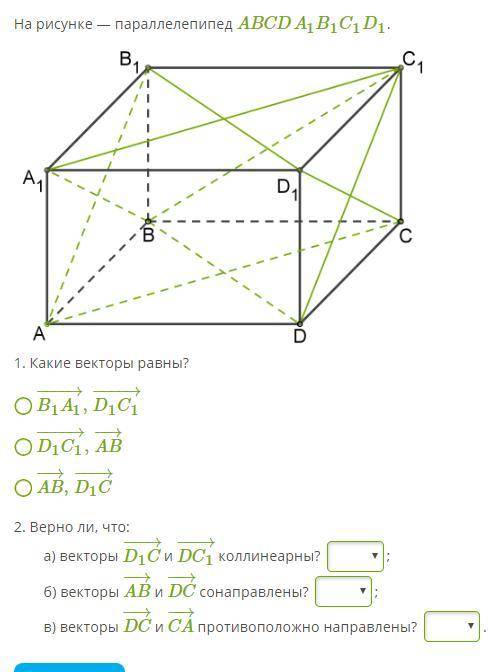
Ответы
2. В данной задаче нам дана плоскость α и наклонная AB, проведенная к этой плоскости. Наша задача - вычислить расстояние от точки B до плоскости α.
Как уже указано в условии, длина наклонной AB составляет 20 см, а наклонная образует угол 45° с плоскостью α.
Для решения этой задачи можно использовать тригонометрию. Заметим, что у нас есть прямоугольный треугольник, в котором гипотенуза равна 20 см, а один из катетов образует угол 45° с гипотенузой. Мы хотим найти другой катет, который представляет расстояние от точки B до плоскости α.
Для начала, найдем длину катета. Так как угол между гипотенузой и одним из катетов равен 45°, а треугольник прямоугольный, то по теореме Пифагора:
катет^2 + катет^2 = гипотенуза^2
Подставляя известные значения, получаем:
катет^2 + катет^2 = 20^2
2 * катет^2 = 400
катет^2 = 200
катет ≈ √200
Таким образом, длина катета (расстояние от точки B до плоскости α) составляет примерно √200 см.
Ответ: Расстояние от точки B до плоскости α равно примерно √200 см.
3. В данной задаче нам дана правильная треугольная пирамида, в которой боковое ребро образует угол 45° с плоскостью основания, а высота пирамиды равна 2 см. Наша задача - вычислить сторону основания пирамиды.
Из условия следует, что высота пирамиды является медианой треугольника, образованного боковым ребром и двумя сторонами основания. По свойствам правильной треугольной пирамиды, медианы являются биссектрисами и могут быть разделены на отрезки, пропорциональные соответствующим сторонам.
Обозначим сторону основания пирамиды через a. Тогда, согласно свойству прямоугольного треугольника и биссектрисы:
a / 2 = 2 / a
Раскроем пропорцию:
a * a = 2 * 2
a^2 = 4
a = √4
Таким образом, сторона основания пирамиды равна √4 см.
Ответ: Сторона основания пирамиды равна √4 см.
4. В данной задаче мы видим параллелограмм ABCD, в котором AB = BC = CD = 4 см и AD = 3 см. Наша задача - вычислить угол BAD.
Для решения этой задачи мы можем использовать свойства параллелограмма, а именно, что противоположные стороны в параллелограмме равны.
Из условия задачи видно, что стороны AB и AD параллельны и равны, что означает, что угол BAD является прямым углом.
Ответ: Угол BAD равен 90°.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Популярные вопросы
- Вчетырехугольнике авсd ав||сd и ав меньше сd. луч ам пересекает сторону...
1 - Серед куплених 16 зошитів було 5 зошитів у лінійку.яку частину всіх...
2 - Определите давление танка массой 55т на землю , если площадь гусеницы...
3 - Вычислительная : 4/210+5/140,7/450+8/180,9/180+7/120=...
1 - Какие породы свиней разводят в красноярском крае? 10...
1 - Материал о взрывах, произведённых террористами в местах массового скопления...
2 - 1.в каком ряду оба наречия образованы одним и тем же ползком,посуху....
1 - Напомните мне старую песню из тысячи ягод на свете малину одну я люблю...
3 - Dlja prigotovlenija varenja mama beret jagodi i sahar 3 k 2. skolko...
3 - 1.посмотрите,какие общественные сословия присутствуют у н.в.гоголя?...
3