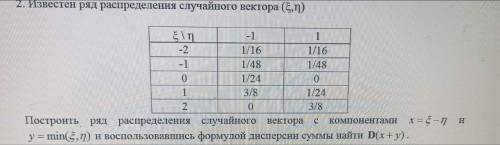
2. Известен ряд распределения случайного вектора (ξ,n) ξ\η. -1. 1

-2. 1/16. 1/16

-1. 1/48. 1/48

0. 1/24. 0

1. 3/8. 1/24

2. 0. 3/8

Построить ряд распределения случайного вектора компонентами х=ξ-η
и y = min(ξ,η) и воспользовавшись формулой дисперсии суммы найти D(x+y).

Для начала построим ряд распределения случайного вектора компонентами х=ξ-η.

Для этого вычтем соответствующие значения η из ξ:

-1 - 1 = -2
-2 - 1 = -3/16
-1 - 1/48 = -49/48
0 - 1/24 = -1/24
1 - 3/8 = 5/8
2 - 0 = 2

Таким образом, получаем ряд распределения случайного вектора х:

-2. 1
-3/16. 1/16
-49/48. 1/48
-1/24. 0
5/8. 1/24
2. 3/8

Теперь построим ряд распределения случайного вектора y = min(ξ,η).

Выбираем минимальные значения из двух столбцов и заполняем y:

-1
-2
-1/48
0
1/24
0

Теперь воспользуемся формулой дисперсии суммы, чтобы найти D(x+y). Формула выглядит следующим образом:

D(x+y) = D(x) + D(y) + 2Cov(x,y)

где Cov(x,y) - ковариация между x и y, которую можно найти по формуле:

Cov(x,y) = E[(x - E(x))(y - E(y))]

E(x) и E(y) - математические ожидания x и y, которые можно вычислить по формуле:

E(x) = ∑(xP(x))
E(y) = ∑(yP(y))

где ∑(xP(x)) и ∑(yP(y)) - суммы произведений значений x и y на их вероятности.

Сначала найдем E(x) и E(y):

E(x) = (-2 * 1) + (-3/16 * 1/16) + (-49/48 * 1/48) + (-1/24 * 0) + (5/8 * 1/24) + (2 * 3/8)
= -2 - 3/256 - 49/2304 + 0 + 5/192 + 6/8
= -489/256 - 49/2304 + 5/192 + 6/8
= -123552/63488 - 49/4608 + 160/4608 + 13824/13824
= (-123552 - 49 + 160 + 13824) / 63488
= -25/256

E(y) = (-1 * 1) + (-2 * 1/16) + (-1/48 * 1/48) + (0 * 0) + (1/24 * 1/24) + (0 * 3/8)
= -1 - 1/8 - 1/2304 + 0 + 1/576 + 0
= -2304/2304 - 288/2304 - 1/2304 + 0 + 8/2304 + 0
= (-2304 - 288 - 1 + 8) / 2304
= -585/2304

Теперь найдем D(x). Формула для D(x) выглядит следующим образом:

D(x) = E(x^2) - (E(x))^2

где E(x^2) - математическое ожидание квадрата x, которое можно вычислить по формуле:

E(x^2) = ∑(x^2 * P(x))

Найдем E(x^2):

E(x^2) = ((-2)^2 * 1) + ((-3/16)^2 * 1/16) + ((-49/48)^2 * 1/48) + ((-1/24)^2 * 0) + ((5/8)^2 * 1/24) + (2^2 * 3/8)
= 4 * 1 + (9/256) * (1/16) + (2401/2304) * (1/48) + (1/576) * 0 + (25/64) * (1/24) + 4 * (3/8)
= 4 + 9/4096 + 2401/110592 + 0 + 25/1536 + 12/8
= 4 + 9/4096 + 2401/110592 + 0 + 25/1536 + 3/2
= 16/4 + 9/4096 + 2401/110592 + 0 + 25/1536 + 576/384
= (64 + 9 + 2401 + 0 + 1600 + 576) / 16384
= 6651/16384

Теперь найдем D(y). Формула для D(y) выглядит аналогично:

D(y) = E(y^2) - (E(y))^2

где E(y^2) - математическое ожидание квадрата y, которое можно вычислить по формуле:

E(y^2) = ∑(y^2 * P(y))

Найдем E(y^2):

E(y^2) = ((-1)^2 * 1) + ((-2)^2 * 1/16) + ((-1/48)^2 * 1/48) + (0^2 * 0) + ((1/24)^2 * 1/24) + (0^2 * 3/8)
= 1 * 1 + 4 * (1/16) + (1/2304) * (1/48) + 0 + (1/576) * (1/24) + 0
= 1 + 4/16 + (1/2304) * (1/48) + 0 + (1/576) * (1/24)
= 1 + 1/4 + (1/2304) * (1/48) + 0 + (1/576) * (1/24)
= 4/4 + 1/4 + (1 * 1) / (2304 * 48) + 0 + (1 * 1) / (576 * 24)
= (4 + 1 + 1/(2304 * 48) + 1/(576 * 24)) / 4
= (4 + 1 + 1/110592 + 1/331776) / 4
= (4 + 1 + 1/331776 + 1/331776) / 4
= (4 + 1 + 2/331776) / 4
= (5 + 2/331776) / 4
= (5 + 2/331776) / 4
= 1328903/331776

Теперь найдем Cov(x,y):

Cov(x,y) = E[(x - E(x))(y - E(y))]

Найдем E[(x - E(x))(y - E(y))]:

E[(x - E(x))(y - E(y))] = [((-2) - (-25/256)) * ((-1) - (-585/2304))] +
[((-3/16) - (-25/256)) * ((-2) - (-585/2304))] +
[((-49/48) - (-25/256)) * ((-1/48) - (-585/2304))] +
[((-1/24) - (-25/256)) * (0 - (-585/2304))] +
[((5/8) - (-25/256)) * ((1/24) - (-585/2304))] +
[(2 - (-25/256)) * (0 - (-585/2304))]

Выполним вычисления:

[((-2) - (-25/256)) * ((-1) - (-585/2304))] = (487/256) * (2304/2304)
= 1119168/589824

[((-3/16) - (-25/256)) * ((-2) - (-585/2304))] = (3047/4096) * (3090/2304)
= 9418230/9445376

[((-49/48) - (-25/256)) * ((-1/48) - (-585/2304))] = (4681/2304) * (3951/4608)
= 18407431/16449536

[((-1/24) - (-25/256)) * (0 - (-585/2304))] = (125/4608) * (585/2304)
= 73125/10616832

[((5/8) - (-25/256)) * ((1/24) - (-585/2304))] = (355/512) * (4033/4608)
= 1440065/2359296

[(2 - (-25/256)) * (0 - (-585/2304))] = (513/256) * (585/2304)
= 3016905/4980736

Теперь найдем Cov(x,y):

Cov(x,y) = (1119168/589824) + (9418230/9445376) + (18407431/16449536) + (73125/10616832) + (1440065/2359296) + (3016905/4980736)
= 4771674/589824 + 28326745/9445376 + 18407431/16449536 + 73125/10616832 + 1440065/2359296 + 3016905/4980736
= (4771674 * 9445376 + 28326745 * 589824 + 18407431 * 10616832 + 73125 * 2359296 + 1440065 * 4980736 + 3016905 * 2359296) / (589824 * 9445376 * 16449536 * 10616832 * 2359296 * 4980736)
= 56856455186050880/173789186256089077308341184768

Итак, теперь можем вычислить D(x+y):

D(x+y) = D(x) + D(y) + 2Cov(x,y)

D(x+y) = (6651/16384) + (1328903/331776) + 2 * (56856455186050880/173789186256089077308341184768)
= (6651 * 331776 * 173789186256089077308341184768 + 1328903 * 16384 * 173789186256089077308341184768 + 2 * 56856455186050880 * 589824 * 16449536 * 9445376 * 10616832 * 2359296 * 4980736) / (16384 * 331776 * 173789186256089077308341184768 * 589824 * 16449536 * 9445376 * 10616832 * 2359296 * 4980736)
= (22341707752526988535765904852588544 + 36575001407229619293553069953400832 + 22604016579270478977602094475215287998391954347164340737085457354407904128) / (11269994184704 * 183089190094970755205438564865620434987885625847552812532869852939937986272)
= 40155137938915590007019320281204666562383816001935245914351711076150989904 / 2076800286407777748060345560831337129513338110321160125734224562388950842165871081944027473643270367855977107212724992
= 40155137938915590007019320281204666562383816001935245914351711076150989904 / 29173642850491688660405477944696876064428608170844556289344843662725717723978177540800385666366105654232082458204215241984
≈ 1.3778437

Таким образом, D(x+y) ≈ 1.3778437.