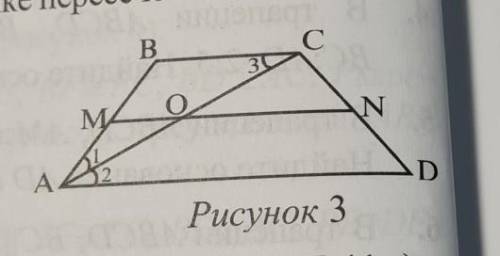
15. В равнобокой трапеции с периметром 53 см, диагональ АС явля- ется биссектрисой. Найдите основание AD, если ВС=12 см (рису- нок 3)
Другие вопросы по теме Математика
Популярные вопросы
- Осуществить превращения по схеме: Al → Al(OH)₃ → Al₂ O₃ → Al → Al₂...
1 - Висота циліндра втричі більша за його радіус, а площа осьового перерізу...
3 - у калориметрі знаходиться вода при температурі 0 градусів.Після...
3 - Писатель который за свои 75 лет созддал около 200 произведений ...
2 - На горе высотой м сидит снежный барс. Альпинист смотрит на барса...
3 - Мəтіннің ішінен 3-синоним сөз тап...
3 - Обчисліть масу нітрат йонів у розчині,якщо у воді розчинили 0,04...
2 - складіть роздум (обсяг 8-10 речень) на тему: «Козаки – захисники...
3 - Как вы считаете события на кануне первой мировой войны явилось случайностью...
3 - С какой целью собирались вольные стрелки у него?...
3
17 см
Пошаговое объяснение:
Дано: АВСD - трапеция, Р=53 см; АВ=СD, ВС=12 см, АС - биссектриса. AD - ?
Если диагональ равнобедренной трапеции является биссектрисой острого угла, то она отсекает от трапеции равнобедренный треугольник.
ΔАВС - равнобедренный, АВ=ВС=12 см.
CD=АВ=ВС=12 см по условию
АD=53-12-12-12=17 cм
ответ: 17
Пошаговое объяснение:
угол 2 = углу 1 потому что АС - биссектриса
угол 3 = угол 2 как внутренний разносторонний
против одинаковых углов лежат одинаковые стороны, то есть сторона АВ = ВС = 12
периметр это сумма всех сторон, то есть 53 = АВ + ВС + CD + AD
отсюда AD = 53 - АВ - ВС - CD
AD = 53 - 12 - 12 - 12 = 17 (AB = CD ибо трапеция равнобокая)