11. Найти частные производные Z'x,Z'y:
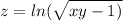
Другие вопросы по теме Математика
Популярные вопросы
- Распредели словосочетания на три группы: «прич. + сущ*.» и «прич.* + сущ.» —накинутый...
1 - Столица Кашкадарынского области...
1 - 3х^2-48=0 найти все корени...
3 - К 100 г р-ра с массовой долей хлорида бария BaCl2 10% добавили изб. р-ра фосфорной...
3 - У коробці міститься 10 білих і 6 чорних куль. Скількома бами з коробки можна витягти:...
3 - Для чего используют флажки?...
2 - Напруга на клемах реостата дорівнює 1,2 В, а опір частини обмотки, в якій тече...
1 - Нужна творческая лабораторная работа по теме Изучение электрического двигателя...
3 - Цитатна характеристика Бермана з новели останній листокБудь ласка мен...
3 - Основні напрямки політики що проводив канцлер Бісмарк ?...
1
Пошаговое объяснение:
сначала производная от логарифма, потом от корня, потом от линейной