11 классе изучают 11 предметов сколькими можно составить расписание на четверг, если должно быть 8 различных уроков и из порядок не важен

Пошаговое объяснение:

Стандартная комбинаторная задача

Есть выбрать первый урок в расписании, для каждого из них есть по выбора второго урока, ... для каждого варианта выбора первых семи уроков есть по 4 варианта выбора последнего урока.

Всего

Но так как порядок не важен, каждый был посчитан по 8! раз - количеству перестановок восьми уроков. Исключим все повторения:

В задаче "выбрать k штук из n объектов, порядок не важен" ответом является число сочетаний из n по k: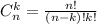

Чтобы решить эту задачу, нужно использовать комбинаторику, а именно принцип комбинаторного умножения.

Для составления расписания на четверг нужно выбрать 8 различных уроков из 11 предметов. Из условия известно, что порядок уроков не имеет значения, то есть, например, математику можно ставить как первым, вторым или любым другим уроком.

Поэтому для каждого предмета мы имеем две возможности: включить его в расписание или не включать. Это дает нам 2 варианта для каждого из 11 предметов. Таким образом, общее количество возможных расписаний будет равно произведению всех вариантов для каждого предмета.

Для вычисления этого произведения мы можем использовать следующую формулу:
2^11, где 2 - количество возможных вариантов для каждого предмета, а 11 - количество предметов.

Таким образом, общее количество возможных расписаний на четверг составит 2^11, то есть 2048.

Обоснование этого решения состоит в том, что мы рассматриваем все возможные комбинации выбора уроков из 11 предметов, при условии, что порядок не важен. Каждый предмет может быть либо выбран, либо не выбран, и это дает нам два варианта для каждого предмета. При умножении этих вариантов мы учитываем все возможные комбинации выбора и получаем итоговое количество расписаний.