1. Математика
  2. 101 × 102 × 103 × 104 × ...

101 × 102 × 103 × 104 × ... × 300 = 7^k × n (k и n - натуральные числа)

Найдите наибольшее значение для k.
А) 26 Б) 29 В) 30 Г) 31 Д) 32

Gok3004 Gok3004    1   17.08.2020 13:50    1

Ответы
delvar25 delvar25  15.10.2020 16:00

101\cdot102\cdot103\cdot104\cdot...\cdot300=7^{k_{\max}}\cdot n

Найдем, сколько чисел от 101 до 300 делятся на 7.

\dfrac{101}{7} =14\dfrac{3}{7}

\dfrac{300}{7} =42\dfrac{6}{7}

Числа от 101 до 300, делящиеся на 7, дают частные от 15 до 42 включительно. Значит, их количество равно:

42-15+1=28

Но, среди чисел от 101 до 300 есть такие, которые делятся на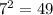 7^2=49. Найдем их количество.

\dfrac{101}{49} =2\dfrac{3}{49}

\dfrac{300}{49} =6\dfrac{6}{49}

Числа от 101 до 300, делящиеся на 49, дают частные от 3 до 6 включительно. Значит, их количество равно:

6-3+1=4

Среди чисел от 101 до 300 делящихся на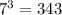 7^3=343, а также на большие степени числа 7 нет.

Значит, 28 чисел имеют сомножитель "7". Кроме этого 4 числа имеют еще один сомножитель "7". Значит, всего сомножителей "7" имеется:

28+4=32

ответ: 32

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
yufhdg yufhdg  29.04.2019 10:15
Решить .в первый день автомобиль проехал 635км это на 127 км меньше чем во второй.в третий день он проехал на 85 км больше чем в первый день.сколько он проехал км за три...
rozettak rozettak  29.04.2019 10:15
Кзавтрашнему дню дали , но я вообще не понимаю что и как тут делать объясните как это сделать и желательно ни в текстовом виде, а в голосовом, вод имеется дискорд, а то...
крис855 крис855  29.04.2019 10:15
Школьников 32% все астольные взрослые. все вместе участники соревнования. взрослых больше чем школьников на 72 человека. сколько было всего участников соревнования...
zaper886 zaper886  29.04.2019 10:16
Водной стопке шестьдесят девять тетрадей, а в другой в 3 раза меньше. сколько тетрадей надо взять из первой стопки для того, чтобы количество тетрадей в двух стопках стало...
yura23424 yura23424  29.04.2019 10:16
Решите уравнение: 8,78x-4,78x=1,2...
bikosh02 bikosh02  29.04.2019 10:17
Номер 1234 номер 1235 и номер 1236​...
Goodsteve31 Goodsteve31  29.04.2019 10:18
Какова вероятность выигрыша в спортивной лотерее 3 из 16 (в лотерее участвуют 16 номеров- с 1-го до 16-го, выигрыш выпадает на 3 номера)? !...
AnnaFruzanna AnnaFruzanna  29.04.2019 10:19
Решите примеры. запиши в виде десятичной дроби: 4,6 % = запиши в процентах: 0,703 = %. запиши десятичные дроби в процентах: 0,81 = %; 0,04 = %. преобразуй данную дробь 810...
snezanakoba snezanakoba  29.04.2019 10:19
Решите первый сделал, дайте второе решение...
romanvailev15 romanvailev15  29.04.2019 10:20
30 ! третий номер,найти композицию​...

Популярные вопросы