[100б Две задачи по прогрессии. Желательно подробнее ,чтобы я поняла)

Заранее большое

(в моих вопросах еще одна задача)

[100б Две задачи по прогрессии. Желательно подробнее ,чтобы я пон

Ответы

Alisa45612 15.10.2020 14:47

29) 192

38) 6

Пошаговое объяснение:

29) Для арифметической прогрессии справедливо соотношение

Сумма членов с номерами 1 и n, равна сумме членов с номерами 2 и (n-1), равна сумме членов с номерами 3 и (n-2) и т.д. То есть если сумма номеров членов последовательности равна n+1, то равны и их суммы.

Ряд составленный из членов с номерами 3,6,9,...,3n это тоже арифметическая прогрессия значит равны суммы членов с такими номерами:

3 и 3n;6 и 3n-3;9 и 3n-612 и 3n-9

То есть, если сумма номеров членов последовательности равна 3n+3, то равны и их суммы. А сумма всех членов последовательности от 3 до 3n с шагом 3 равна сумме первого и последнего, т.е n и 3n умноженное на количество таких пар, а оно равно n/2

Складываем 2n+1 и n+2, эта сумма равна 3n+3

Значит a3+a6+a9+...a3n=(a[2n+1] + a[n+2])*n/2=23*n/2=736

n=736*2/23=64

А количество членов арифметической прогрессии равно 3*64=192

38) Функция 3+5x-x^2 достигает своего максимума в точке, которая является центром отрезка [x1,x2], где x1,x2 это корни квадратного уравнения 3+5x-x^2=0. По теореме Виета сумма корней приведенного квадратного уравнения равна коэффициенту перед первой степенью x со знаком минус. В нашем случае это 5, тогда функция принимает максимальное значение при x=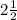 $2\frac{1}{2}$ . Найдем член последовательности при n=2 он равен 9,при n=3 он тоже равен 9.