(100 ) составить неявные и параметрические уравнения плоскости, проходящей через точки с( 1; 1; 3), a(3; 2; 1), b(2; 4; 6).
Другие вопросы по теме Математика
Популярные вопросы
- Велосипедист спускается с горы с постоянным ускорение 0,8 м/с. какова...
3 - Гетерогенной реакцией является реакция взаимодействия кислорода...
2 - Составьте 7 предложений в повелительном наклонении на...
1 - Как ты думаешь можно ли одним предложением охарактеризовать человека...
3 - Масса железного бруска длиной 3,5 м равна 8 3/4 кг.от этого железного...
1 - Светофор жайлы жұмбақ құрастыру керек ....
1 - Отметьте на координатном луче все точки координаты натуральные числа...
3 - Длина прямоугольника 4см,а ширина на в 4 раза меньше...
1 - Бір топ жазғы демалыста тауға серуенге шықты синтаксический...
3 - Найдите значение выражения: 1/5+1/7-1/9 13/18-1/24-(29/72+6/36)...
2
Параметрические уравнения:
Неявное уравнение:
Пошаговое объяснение:
Параметрическое уравнение
Вектор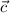 :
:
Вектор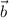 :
:
Берём, скажем, точку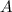 как отправную, и размножаем векторы
как отправную, и размножаем векторы 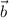 и
и 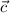 , используя параметры
, используя параметры  и
и 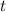 :
:
Отсюда параметрические уравнения:
Неявное уравнение
В уравнении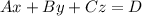 коэффициенты A, B, C - это координаты вектора нормали, а D - коэффициент, сдвигающий плоскость, задаваемую вектором нормали, так, чтобы плоскость содержала в себе одну из точек из условия.
коэффициенты A, B, C - это координаты вектора нормали, а D - коэффициент, сдвигающий плоскость, задаваемую вектором нормали, так, чтобы плоскость содержала в себе одну из точек из условия.
Найдём вектор нормали как векторное произведение векторов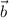 и
и 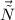 :
:
Итого
Предварительный вид неявного уравнения:
Найдём D, подставив какую-нибудь из точек из условия, скажем, С:
Итого: