1. Математика
  2. 100 ! найдите максимально возможный

100 !
найдите максимально возможный остаток от деления квадратного трехчлена -х^2-x+13 на линейный многочлен 4x-a (при всевозможных вещественных значениях параметра a). ответ цифрами

AlyaMrr AlyaMrr    3   25.10.2019 18:30    6

Ответы
makrona123 makrona123  10.10.2020 09:43

13\frac{1}{4}

Пошаговое объяснение:

Делим многочлены угольком. Получим следующий остаток (деление на приложенном рисунке) и преобразуем его вид:

13-\frac{a}{4}(1+\frac{a}{4}) =13-(\frac{a}{4}+(\frac{a}{4})^{2})=

=13-(2*\frac{1}{2}* \frac{a}{4}+(\frac{a}{4})^{2})=13-(-(\frac{1}{2} )^{2}+(\frac{1}{2} )^{2}+2*\frac{1}{2}* \frac{a}{4}+(\frac{a}{4})^{2})=

=13+(\frac{1}{2} )^{2}-((\frac{1}{2} )^{2}+2*\frac{1}{2}* \frac{a}{4}+(\frac{a}{4})^{2})=13+\frac{1}{4} -(\frac{1}{2} +\frac{a}{4})^{2}=

=13\frac{1}{4} -(\frac{1}{2} +\frac{a}{4})^{2}

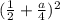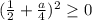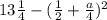Последнее выражение остатка, т.е. разность принимает максимально возможное значение, когда (\frac{1}{2} +\frac{a}{4})^{2} принимает минимально возможное значение. Но (\frac{1}{2} +\frac{a}{4})^{2}\geq 0 и поэтому его минимально возможное значение равно 0. Значит,  максимально возможное значение выражения 13\frac{1}{4} -(\frac{1}{2} +\frac{a}{4})^{2} - это 13\frac{1}{4}


100 ! найдите максимально возможный остаток от деления квадратного трехчлена -х^2-x+13 на линейный
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
ольга591 ольга591  09.07.2019 13:20
Укажите число которое без остатка не делится на 7 1)56 2)48 3)35 4)21...
lava777pop lava777pop  09.07.2019 13:20
Найдите значение суммы: 1)-5/7+4/7; 2)-5/8+7/8; 3) -1/6+1; 4) 5/12-1/12; 5) 7/15-11/15; 6) 5/16-1/6....
StasyaSelyugina StasyaSelyugina  09.07.2019 13:20
Сообщение на тему свет и тепло в жизни растений...
Lyashchyov4777 Lyashchyov4777  09.07.2019 13:20
Папа собрал в два раза больше грибов, чем мама, а дочь в четыре раза больше, чем папа, но на три гриба меньше, чем её брат лёша. сколько грибов собрала мама, если лёша собрал восемьдесят...
Филипсия Филипсия  09.07.2019 13:20
Увеличь число 5 в 24 число 24 в виде произведения трёх множителей....
Darina0090 Darina0090  09.07.2019 13:20
А.на отрезке ав отметьте точки с и d.сколько отрезков получилось? б.постройте острый угол аов.проведите внутри этого угла два луча od b oe.сколько острых углов получилось? 11 быллов...
mgarkanov mgarkanov  09.07.2019 13:20
Собрали 48 кг слив. на варенье истратили в 8 раз меньше. сколько кг слив осталось?...
LPKenion LPKenion  09.07.2019 13:20
Кто по должности осуществляет руководство комиссия по чрезвычайным ситуациям объекта ? какие уровни включает в себя гражданская оборона россии? какое количество основных в области...
SaySasha02 SaySasha02  09.07.2019 13:20
Вычисли периметр треугольника,длины сторон которого равны 2дм 6см, 5дм, 3дм 8см. ....
Ksyusha891 Ksyusha891  09.07.2019 13:20
Встопке было 35 тетрадей. 5 учеников взяли из нее по 6 тетрадей. сколько тетрадей осталось?...

Популярные вопросы