10 корней из 2 × cos^2(15п/8)-5 корней из 2
Ответы
Воспользуемся формулой понижения степеней 
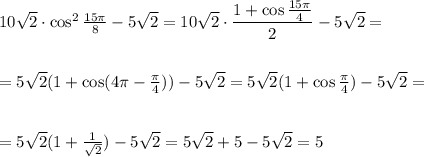
ПОКАЗАТЬ ОТВЕТЫ


Другие вопросы по теме Математика
Популярные вопросы
- Анализ метафоры сердце пусто. ...
3 - Опера-це музична вистава,де: -багато співають-багато танцюють-багато...
2 - Обчисліть значення виразу найзручнішим...
1 - В парке высадили деревья. Березы - 2/5, клены - 1/4, липы - 3/20, а дубы...
3 - 207. Сума двох відповідних кутів, що утворилися при пере- тині двох паралельних...
3 - Обчисліть масу води яку можна нагріти від 0° до 100° повністю спаливши...
2 - Если известно, что 0,(72) = 8/11, то преобразуйте переодическую десчтичную...
2 - решить эти задания, плачу много, ответы с решением...
1 - 25*27=11 30*38=6 11*11=10 19*30=?...
2 - Какие равные элементы необходимо добавить, чтобы треугольники на рисунке...
2