Математика: 10 - 2 1/2 : 3 3/4 + (2 1/2 - 1 1/3) * 6=

10 - 2 1/2 : 3 3/4 + (2 1/2 - 1 1/3) * 6=

Ответы

nazipovadk 29.03.2022 17:00

16 1/3

Пошаговое объяснение:

10 - 2 1/2 : 3 3/4 + (2 1/2 - 1 1/3) * 6= 10 - 5/2 : 15/4 + (5/2 - 4/3) * 6=

=10 - 5/2 * 4/15 + 7/6 * 6 = 10 - 2/3 +7 = 16 1/3

ПОКАЗАТЬ ОТВЕТЫ

scorpu 29.03.2022 17:00

$\large \boldsymbol {} \bf 16\dfrac{1}{3} .$

Пошаговое объяснение:

Перепишем исходное выражение:

$\displaystyle10-2\frac{1}{2} :3\frac{3}{4} +\bigg(2\frac{1}{2} -1\frac{1}{3}\bigg)\cdot6.$ Нужно вычислить значение выражения.

Решение: Во-первых, представим смешанные числа в виде неправильных дробей.

Правило: Результатом преобразования смешанной дроби в неправильную дробь будет дробь числитель, которой равен сумме произведения целой части на знаменатель дроби с числителем смешанной дроби, а знаменатель остается прежним.Это можно записать короче в виде формулы: $\boxed{\displaystyle a\frac{b}{c} =\frac{c\cdot a+b}{c} } .$

В нашем случае: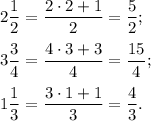 $\displaystyle2\frac{1}{2} =\frac{2\cdot2+1}{2} =\frac{5}{2} ;3\frac{3}{4} =\frac{4\cdot3+3}{4} =\frac{15}{4} ;1\frac{1}{3} =\frac{3\cdot1+1}{3} =\frac{4}{3} .$

Выражение приняло вид: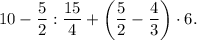 $\displaystyle10-\frac{5}{2} :\frac{15}{4} +\bigg(\frac{5}{2} -\frac{4}{3} \bigg)\cdot 6.$

Первое действие - то, что в скобках.

Правило: Чтобы найти разность двух дробей с разными знаменателями, надо привести их к общему положительному знаменателю и выполнить вычитание дробей с одинаковыми знаменателями.

$\displaystyle1)~~\frac{5^{(3} }{2} -\frac{4^{(2} }{3} =\frac{(5\cdot3)-(4\cdot2)}{2\cdot3} =\frac{15-8}{6} =\frac{7}{6} .$

Выражение приняло вид:

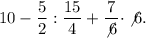$\displaystyle10-\frac{5}{2} :\frac{15}{4} +\frac{7}{\not6} \cdot\not6.$ Преобразуем.

Правило: Чтобы разделить дробь на дробь, нужно деление заменить умножением, вторую дробь "перевернуть". ⇒

$\displaystyle10-\frac{\not5}{\not2} \cdot\frac{\not4^2}{\underbrace{15}_{\not5\cdot3} } +7=10-\frac{2}{3} +7=17-\frac{2}{3} =\frac{51-2}{3} =\frac{49}{3} =\boxed{16\frac{1}{3} } .$