1)Записать уравнение плоскости по трём точкам А, В, с, если А(7; -1; -2), В(1; 7; 8), С(3; 7; 9). 2)Найти уравнение прямой
3)Доказать, что векторы a, b, c образуют базис и записать вектор d в базисе (a, b, c), если a(-1, 2, -3); b(0, 2, 4); c(3, -1, 4) и d(-2, 3, 2)

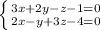
$\left \{ {{3x+2y-z-1=0} \atop {2x-y+3z-4=0}} \right.$

Ответы

Xxxmara 15.02.2022 12:56

1)Записать уравнение плоскости по трём точкам А, В, с, если

А(7; -1; -2), В(1; 7; 8), С(3; 7; 9).

2)Найти уравнение прямой

3)Доказать, что векторы a, b, c образуют базис и записать вектор d в базисе (a, b, c), если a(-1, 2, -3); b(0, 2, 4); c(3, -1, 4) и d(-2, 3, 2).

1) Для составления уравнения плоскости используем формулу:

x - xA y - yA z - zA

xB - xA yB - yA zB - zA

xC - xA yC - yA zC - zA = 0

Подставим данные и упростим выражение:

x – 7 y - (-1) z - (-2)

1 – 7 7 - (-1) 8 - (-2)

3 – 7 7 - (-1) 9 - (-2) = 0

x – 7 y - (-1) z - (-2)

-6 8 10

-4 8 11 = 0

(x – 7 )(8·11-10·8) - (y - (-1))((-6)·11-10·(-4)) + (z - (-2))((-6)·8-8·(-4)) = 0

8(x – 7) + 26(y - (-1)) + (-16)(z - (-2)) = 0

8x + 26y - 16z - 62 = 0

4x + 13y - 8z - 31 = 0.

2) Дана прямая d как линия пересечения плоскостей:

{3x+2y-z-1=0; 2x-y+3z-4=0)

Направляющий вектор “p” нашей прямой ортогонален нормальным векторам n1 и n2 плоскостей. А если , то вектор «p» найдём как векторное произведение векторов нормали: .

Из уравнений плоскостей {(3x+2y-z-1=0; 2x-y+3z-4=0) снимаем их векторы нормали:

n1(3; 2; -1), n2(2; -1; 3).

И находим направляющий вектор p прямой d, перпендикулярный двум заданным с векторного произведения.

I j k| I j

3 2 -1| 3 2

2 -1 3| 2 -1 = 6i - 2j - 3k - 9j - 1i – 4k = 5i - 11j - 7k.

Вектор p = (5; -11; -7).

Можно применить готовую формулу для определения направляющего вектора линии пересечения двух плоскостей.

p ⃗(|(B_1&[email protected]_2&C_2 )||(C_1&[email protected]_2&A_2 )||(A_1&[email protected]_2&B_2 )|)

p = (2*3 – (-1)*(-1); -1*2-3*3; 3*(-1)-2*2) = (5; -11; -7).

Далее надо найти точку на прямой.

Так как линия пересекает плоскость хОу, то в этой точке координата z = 0.

Поэтому в системе уравнений нужно обнулить координату z.

Пусть z = 0, тогда получаем систему двух линейных уравнений с двумя неизвестными: {([email protected]=0) {([email protected]=0)

Почленно складываем уравнения и находим решение системы:

7x - 9 = 0,

x = 9/7,

y = 2х – 4 = 2(9/7) – 4 = -10/7.

Таким образом, точка M((9/7); (-10/7); 0) принадлежит данной прямой.

Выполним проверку: подставим координаты точки M((9/7); (-10/7); 0) в исходную систему уравнений:

{(3(9/7)+2(-10/7)-0-1=27/7-20/7-7/7=0; 2(9/7)-(-10/7)+3*0-4=18/7+10/7-28/7=0)

Получены верные равенства, значит, действительно, M ∈ d.

Тогда по точке M((9/7); (-10/7); 0) и направляющему вектору p=(5; -11; -7) составляем уравнение прямой:

(x-(9/7))/5 = (y + (10/7))/(-11) = z/(-7).

3) Даны векторы a(-1;2;-3), b(0;2;4), c(3;-1;4), d(-2;3;2).

Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора d в этом базисе.

Данная задача состоит из двух частей. Сначала необходимо проверить образуют ли векторы базис. Векторы образуют базис, если определитель, составленный из координат этих векторов, отличен от нуля, в противном случае вектора не являются базисными и вектор d нельзя разложить по данному базису.

Вычислим определитель матрицы:

E = -1 2 -3

0 2 4

3 -1 4

∆ = -1*(2*4 - (-1)*4) - 0*(2*4 - (-1)*(-3)) + 3*(2*4 - 2*(-3)) = 30.

Определитель матрицы равен ∆ =30.

Так как определитель отличен от нуля, то векторы образуют базис, следовательно, вектор X можно разложить по данному базису. Т.е. существуют такие числа α1, α2, α3, что имеет место равенство:

X = α1*a + α2*b + α3*c.

Запишем данное равенство в координатной форме:

(-2;3;2) = α(-1;2;-3) + α(0;2;4) + α(3;-1;4).

Используя свойства векторов, получим следующее равенство:

(-2;3;2) = (-1α1;2α1;-3α1;) + (0α2;2α2;4α2;) + (3α3;-1α3;4α3;)

(-2;3;2) = (-1α1 + 0α2 + 3α3;2α1 + 2α2 -1α3;-3α1 + 4α2 + 4α3)

По свойству равенства векторов имеем:

-1α1 + 0α2 + 3α3 = -2

2α1 + 2α2 -1α3 = 3

-3α1 + 4α2 + 4α3 = 2

Решаем полученную систему уравнений методом Крамера.

Dx1 = -2 0 3