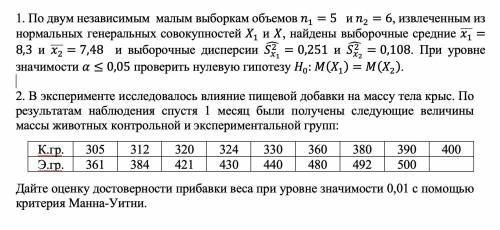
1 задание: По двум независимым малым выборкам объемов n_1=5 и n_2=6, извлеченным из нормальных генеральных совокупностей X_1 и X, найдены выборочные средние ¯(x_1 )=8,3 и ¯(x_2 )=7,48 и выборочные дисперсии (S_(x_1)^2 ) ̂=0,251 и (S_(x_2)^2 ) ̂=0,108. При уровне значимости α≤0,05 проверить нулевую гипотезу H_0: M(X_1 )=M(X_2 ).
2 задание: В эксперименте исследовалось влияние пищевой добавки на массу тела крыс. По результатам наблюдения спустя 1 месяц были получены следующие величины массы животных контрольной и экспериментальной групп:
К.гр. 305 312 320 324 330 360 380 390 400
Э.гр. 361 384 421 430 440 480 492 500
Дайте оценку достоверности прибавки веса при уровне значимости 0,01 с критерия Манна-Уитни.
Другие вопросы по теме Математика
Популярные вопросы
- 483. Исправьте ошибки в написании на-речий. Запишите исправленные предложе-ния.1....
2 - Перепишите текст, раскрывая скобки, вставляя, где это необходимо, пропущенные...
3 - Complete the sentences. (составить предложения со словами, которые даны ниже)...
3 - Дайте письменный ответ на во островский позамствовал сюжет из русских народных...
3 - Вычислить значение функции: f(x)=(2+3x)^4 в точке x=1,05 помагите...
2 - Кто родители шүкүрбека бейшеналиева?...
2 - Выразите из каждого уравнения а)переменную х б)переменную у 1) 2х – 4у =...
2 - Используя дополнительную литературу интернет ресурсы назовите фамилию и должность...
1 - The waiter is bringing it now составьте 5 типов во к предложению...
3 - Выполни тест по теме урока: 1. Укажите причины возникновения близорукости:...
3
Для проверки гипотезы о равенстве математических ожиданий двух генеральных совокупностей можно воспользоваться двувыборочным критерием для независимых выборок. В данном случае у нас есть две малые выборки объемом n_1=5 и n_2=6, выборочные средние равны ¯(x_1 )=8,3 и ¯(x_2 )=7,48, а выборочные дисперсии равны (S_(x_1)^2 ) ̂=0,251 и (S_(x_2)^2 ) ̂=0,108.
Шаг 1: Сформулируем нулевую и альтернативную гипотезы:
H_0: M(X_1 )=M(X_2 ) (математические ожидания двух генеральных совокупностей равны)
H_1: M(X_1 )≠M(X_2 ) (математические ожидания двух генеральных совокупностей не равны)
Шаг 2: Установим уровень значимости α≤0,05.
Шаг 3: Вычислим статистику критерия T:
T = (¯(x_1 ) - ¯(x_2 )) / sqrt((S_(x_1)^2 / n_1) + (S_(x_2)^2 / n_2))
Подставим значения:
T = (8,3 - 7,48) / sqrt((0,251 / 5) + (0,108 / 6))
T ≈ 1,383
Шаг 4: Найдем критическую область. У нас двусторонняя альтернативная гипотеза, поэтому критическая область будет состоять из двух хвостов по α/2 каждый.
Найдем критическое значение t:
t_krit = t(alpha/2, n_1 + n_2 - 2)
Находим t_krit для α/2 = 0,05/2 = 0,025 и степеней свободы df = n_1 + n_2 - 2 = 5 + 6 - 2 = 9:
t_krit ≈ 2,262
Шаг 5: Сравниваем значение статистики критерия T с критическим значением t_krit. Если T попадает в критическую область, то отвергаем нулевую гипотезу, иначе не отвергаем.
В данном случае T = 1,383 < 2,262, поэтому не отвергаем нулевую гипотезу.
2 задание:
Для оценки достоверности прибавки веса при уровне значимости 0,01 с критерия Манна-Уитни можно воспользоваться ранговым критерием.
Шаг 1: Соединим две выборки в одну выборку и рассчитаем ранги для каждого значения, включая повторяющиеся значения.
К.гр.: 305 312 320 324 330 360 380 390 400
Э.гр.: 361 384 421 430 440 480 492 500
Объединенная выборка: 305 312 320 324 330 360 380 390 400 361 384 421 430 440 480 492 500
Рассчитаем ранги для значений выборки, учитывая повторяющиеся значения:
Ранги для значений К.гр.: 1 2 3 4 5 6 7 8 9
Ранги для значений Э.гр.: 10 11 12 13 14 15 16 17
Шаг 2: Вычислим значение U для каждой выборки:
U_1 = n_1 * n_2 + n_1 * (n_1 + 1) / 2 - R_1
U_2 = n_1 * n_2 + n_2 * (n_2 + 1) / 2 - R_2
Подставим значения:
U_1 = 5 * 8 + 5 * (5 + 1) / 2 - 45 = 64
U_2 = 6 * 8 + 6 * (6 + 1) / 2 - 90 = 66
Шаг 3: Найдем значение U_0 для нулевой гипотезы, где U_0 = n_1 * n_2 / 2. В данном случае U_0 = 5 * 6 / 2 = 15.
Шаг 4: Найдем критическую область. У нас двусторонняя альтернативная гипотеза, поэтому критическая область будет состоять из двух хвостов по α/2 каждый.
Найдем критическое значение U для α/2 = 0,01/2 = 0,005:
U_krit = n_1 * n_2 - U(alpha/2) + 1
Находим U_krit для α/2 = 0,005 и n_1 * n_2 = 5 * 6 = 30:
U_krit = 30 - U(0,005) + 1
По таблице критических значений критерия Манна-Уитни для выборок объемом до 10 и уровнем значимости 0,01/2 = 0,005 получаем U(0,005) = 53.
Подставляем значения:
U_krit = 30 - 53 + 1 = -22
Шаг 5: Сравниваем значение U для каждой выборки с критическим значением U_krit.
В данном случае U_1 = 64 > -22 и U_2 = 66 > -22, поэтому не отвергаем нулевую гипотезу.
Таким образом, при уровне значимости 0,01 оценка достоверности прибавки веса для экспериментальной и контрольной групп не является статистически значимой.