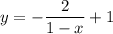(1-x)dy-(y-1)dx=0 найти частные решения дифференциальное уравнений если y=3 при x=2
Другие вопросы по теме Математика
Популярные вопросы
- Из двух посёлков,расстояние между которыми 138 км одновременно навстречу...
1 - «короткий рассказ на тему» мы говорим на языке семьи...
3 - Решить а) 3 1/2*8 1/3*3/25*5*6 1/4*16 б) 1 1/24: 3 1/8: 8/15*3 7/9*1...
3 - Г) 2 4/5 * 5/8 - 1 1/5 * 5/8 д) 5 5/7 * 5/12 * 5 1/4 * 6\7 : 1 1/2...
2 - Мне нужно сделать кроссворд по новой 7 класс 24 параграф из 14...
2 - Як узнати площу? наприклад ширина 12 см а довжина 24см....
3 - 10 предложений со словами nice – nicely, quick – quickly, beautiful...
1 - Как называется достижение цели за счет ущемления интересов отдельного...
1 - Проверьте гласные буквы с однокоренных слов. например-( скрипеть-...
1 - Complete the sentences. use the present simple passive form of the...
1
Это дифференциальное уравнение с разделяющимися переменными.
Получили общее решение дифференциального уравнения.
Найдем теперь частное решение, подставляя начальные условия
Частное решение: