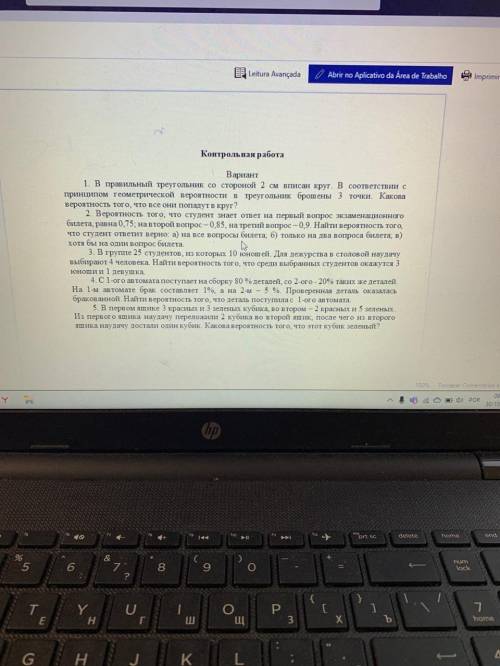
1. В правильный треугольник со стороной 2 см вписан круг. В соответствии с принципом геометрической вероятности в треугольник брошены 3 точки. Какова

вероятность того, что все они попадут в круг?

Для решения данной задачи, нам необходимо разделить область в которой производится бросание точек на две. Сначала определим, куда могут попасть точки: внутрь круга или вне круга.

Рассмотрим наш правильный треугольник со стороной 2 см. Радиус вписанного круга можно найти, используя свойства равностороннего треугольника. Внутри равностороннего треугольника, проведенная к высоте является медианой и делит основание на две равные части. Таким образом, получаем два прямоугольных треугольника внутри равностороннего треугольника. Длина гипотенузы одного из таких прямоугольных треугольников равна радиусу круга, а длина половины основания равна стороне равностороннего треугольника, деленной на 2. Значит, радиус вписанного круга равен 2 см / 2 = 1 см.

Теперь оценим максимальную площадь, в пределах которой могут находиться выпавшие точки. Эта площадь равна площади нашего треугольника со стороной 2 см минус площадь круга радиусом 1 см.

Площадь треугольника с помощью формулы Герона равна:
S = sqrt(p * (p - a) * (p - b) * (p - c)), где a, b, c - стороны треугольника, p - полупериметр (p = (a + b + c) / 2).

Для правильного треугольника со стороной 2 см, полупериметр равен:
p = (2 + 2 + 2) / 2 = 3.

Подставим значения в формулу и вычислим площадь треугольника:
S = sqrt(3 * (3 - 2) * (3 - 2) * (3 - 2)) = sqrt(3) см².

Таким образом, максимальная площадь области, в пределах которой могут находиться выпавшие точки, равна sqrt(3) см².

Далее, будем считать, что точки выпадают равномерно и независимо друг от друга внутри треугольника.

Вероятность того, что точка попадет внутрь круга, можно выразить как отношение площади круга к площади треугольника:
P(круг) = S(круг) / S(треугольник).

Площадь круга равна pi * r^2, где pi - число пи (примерно 3,14), r - радиус круга.
P(круг) = (pi * r^2) / sqrt(3) см².

Подставляем значения:
P(круг) = (3.14 * 1^2) / sqrt(3) ≈ 3.14 / 1.732 ≈ 1.813.

Значит, вероятность того, что все три точки попадут внутрь круга равна (1.813)^3 ≈ 5.080.

Итак, вероятность того, что все три точки попадут внутрь круга составляет примерно 5.080 или около 50.8%.