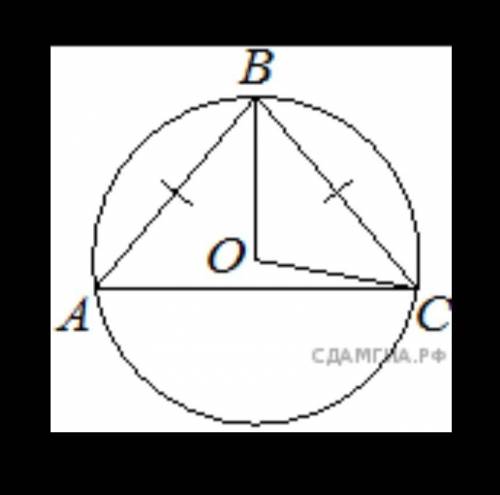
1. В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 70°. Найдите угол ACB. ответ дайте в градусах. 2. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=82°. Найдите угол BOC. ответ дайте в градусах.
Вспомнить свойства равнобедренного треугольника про биссектрису. А так же про равенство углов при основании.
Другие вопросы по теме Математика
Популярные вопросы
- 1) индустриальное общество 19 века. (великобритания, франция, германия, usa) должно...
1 - Решите уравнение(х-5) (х+5)=(х-3)во 2-й степени+2...
2 - Мне подобрать какой нибудь нормальный фоторедактор.чтобы работал без интернета,...
3 - Вкакой части украины находится николаевская область ? завтра контрольная а на этот...
2 - Знайдіть площу паралелограма, дві сторони якого дорівнюють 5√3 см і 2 см та утворюють...
2 - 1.что такое озоновые дыры и чем они опасны? 2.оцените состояние атмоферы в городе,...
3 - Произведение двух чисел равно 8.95. один из множителей умножили на 2.5, а в другой--на...
3 - Укажи слова с согласными на конце слова ко(т,д),сно(п,б),го(т,д),е(ж,ш),стол(п,б),ер(ж,ш)...
2 - Как называется период в северной америки между основанием первой колонии и провозглашением...
3 - Какая масса водорода выделится при взаимодействии цинка с соляной кислотой массой...
1
1. Для нахождения угла ACB нам дано, что отрезки AC и BD являются диаметрами окружности с центром в точке O. Также нам дано, что угол AOD равен 70°.
Угол AOD является центральным углом, соответствующим дуге AD. По свойству центрального угла, такой угол равен половине центрального угла, соответствующего той же дуге. Таким образом, угол ACB будет равен половине угла AOD.
Угол ACB = 70° / 2 = 35°.
Ответ: угол ACB равен 35°.
2. Мы имеем равнобедренный треугольник ABC с углом ABC равным 82° и сторонами AB и BC, равными друг другу.
Так как треугольник равнобедренный, угол BAC также будет равен 82°.
Треугольник ABC описан около окружности с центром в точке O. Таким образом, дуга BC является углом при основании треугольника BOC.
Угол BOC равен половине угла при основании треугольника BOC, то есть половине дуги BC.
Так как угол ABC равен 82°, то угол при основании треугольника BOC равен 180° - 82° - 82° = 16°.
Угол BOC равен половине угла при основании треугольника BOC:
Угол BOC = 16° / 2 = 8°.
Ответ: угол BOC равен 8°.
В данной задаче мы использовали свойства равнобедренного треугольника о биссектрисе и свойство равенства углов при основании треугольника.
Если возникнут дополнительные вопросы или нужно дополнительное объяснение, обращайтесь!