1) сколькими можно в группе из 21 студента выбрать старосту, заместителя старосты,физорга. 2) порядок поступлений 9 участников конкурса определяется жеребьевкой.сколько вариантов жеребьевки при этом возможно. 3) в семье 2 детей.найти вероятность того, что старший ребенок мальчик. 4) в урне 4 белых и 6 черных шаров, из урны по очереди извлекают 2 шара.найти вероятность того, что вынутые шары 1 цвета.

Ответы

Дашка5милашка 04.10.2020 12:41

1) Сколькими можно в группе из 21 студента выбрать старосту, заместителя старосты,физорга.

Старостой может быть выбран любой из 21 студентов,

заместителем - любой из оставшихся 20, а физоргом – любой из оставшихся 19 студентов, т.е.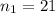 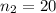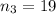n_1=21 , n_2=20 , n_3=19 . По правилу умножения общее число выбора старосты,

его заместителя и физорга равно

N= n_1*n_2*n_3=21*20*19=7980

2) Порядок поступлений 9 участников конкурса определяется жеребьевкой.Сколько вариантов жеребьевки при этом возможно.

Число перестановок

9!=9*8*7*6*5*4*3*2*1=362 880

3) В семье 2 детей.Найти вероятность того, что старший ребенок мальчик.

Варианты детей в семье ММ, МД, ДМ, ДД.

Вероятность определяется по формуле

$P= \frac{m}{n}$

где m- количество благоприятных событий

n- всего событий

В нашем случае m=2, n=4

$P= \frac{2}{4}=0,5$

4) в урне 4 белых и 6 черных шаров, из урны по очереди извлекают 2 шара.Найти вероятность того, что вынутые шары 1 цвета.

Решение

Решим задачу решается применив формулу классической вероятности.

$P=\frac{m}{n}$

m - число благоприятных событий

n - число всех возможных событий

Для этого определим в начале число всех возможных событий n равных числу выбрать два шара из десяти имеющихся

$n=C^2_{10}=\frac{10!}{(10-2)!\cdot 2!}=\frac{10!}{8!\cdot 2!}=\frac{8!\cdot9\cdot10}{8!\cdot 2!}=\frac{90}{2}=45$

Далее определим число m - число благоприятных вариантов вынуть два белых и два черных шара по правилу суммы

$m=C^2_{4}+C^2_{6}=\frac{4!}{(4-2)!\cdot 2!}+\frac{6!}{(6-2)!\cdot 2!}=\frac{2!\cdot3\cdot4}{2!\cdot2!}+\frac{4!\cdot5\cdot6}{4!\cdot2!}=\frac{12}{2}+\frac{30}{2}=6+15=21$