1. [ ) Решите задачу с уравнения. Ширина прямоугольника на 4 см меньше длины, а его площадь 60 см? Найдите стороны и периметр прямоугольника. тоо тола

accolic 1 10.03.2022 23:18 2

Question

Математика: 1. [ ) Решите задачу с уравнения. Ширина прямоугольника на 4 см меньше длины, а его площадь 60 см? Найдите стороны и периметр прямоугольника. тоо тола

accolic · Answer

Пусть ширина прямоугольника равна x, тогда (по условию) длина прямоугольника равна x+4

Площадь прямоугольника равна проиведению его ширины и длины. По условию площадь равна 60 см^2. Тогда имеем уравнение:

$x * (x+4) = 60\\x^2 + 4x - 60 = 0\\D = b^2 - 4ac = 16 + 240 = 256\\\sqrt{D} = \sqrt{256} = 16\\x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{-4 + 16}{2} = 6\\x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{-4 - 16}{2} = -10$

Но ширина прямоугольника не может быть отрицательным числом, поэтому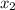 x_2 нам не подходит. Значит ширина прямоугольника равна 6 см. Его длина тогда равна 6+4=10 см

Периметр прямоугольника равен удвоенной сумме его ширины и длины. То есть P = 2 * (6 + 10) = 32 см

ответ: ширина равна 6 см, длина равна 10 см, периметр равен 32 см

1. [ ) Решите задачу с уравнения. Ширина прямоугольника на 4 см меньше длины, а его площадь 60 см? Найдите стороны и периметр прямоугольника. тоо тола

Популярные вопросы