1) решите уравнение 12/y=y-1 и выполнить проверку. 3) определить координаты точки пересечения графиков функций y=2x+6 и y=-3x+1 (без графиков) 3) сравните по величине (5,6 -1/3)/2,2 и |(-1/4 +7)|/2,7. 4)докажите, что значение выражения 15^m / (3^m
* 5^(m+2) + 3^m * 5^m
Другие вопросы по теме Математика
Популярные вопросы
- В сложносочиненном предложении различают и части. ...
1 - Моє ставлення до меценатства-7речень-7речень...
3 - 2. Виберіть агрегатний стан, при якому легко змінити форму речови-...
2 - Морфологический разбор в слове ( Ночная...
3 - встречается ли симметрии в природе? Назовите симметричные объекты,...
3 - 10) При взвешивании фруктов в магазине оказалось, что яблоко тяжелее...
2 - Из квадратного листа фанеры со стороной 78 см вырезали прямоугольник...
3 - упражнение 25 Прочитайте Определите главную мысль текста Озаглавьте...
3 - 82. Луч ОС проходит внутри угла АОВ. Вычислите величину угла АОВ,если...
3 - Вставити пропущену голосну (е чи и ): Вер...сень, віт...рець, кр...вавий,...
1
1)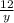 = y-1
= y-1
12-y^2+y=0
y^2-y-12=0
D=b^2-4ac=1+4*12*1=49
y1= (1+7)/2=4
y2=(1-7)/2=-3
проверка
12/4=4-1 или 12/(-3)=-3-1
3=3 -4=-4
2) y=2x+6
y=-3x+1
2x+6=-3x+1
2x+3x=1-6
5x=-5
x=-1
y=4
(-1;4)
3)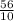 -
- 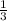 /
/ 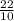 =
= 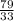
значит (5,6 -1/3)/2,2 < |(-1/4 +7)|/2,7.