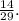1) рабочий обслуживает 3 станка, работающих независимо друг от друга. вероятность того, что в течение часа первый станок не потребует внимания рабочего - 0,9, для второго - 0,8 и для третьего - 0,85. найти вероятность того, что в течение часа хотя бы один станок потребует внимания рабочего. 2) из поступивших на сбору деталей 70% изготовлены автоматом, 2% брака, а 30% - автоматом, 5%брака. наудачу взятая деталь,оказалась бракованной. найти вероятность того, что она изготовлена первым автоматом.

1. Вероятность того, что в течении часа ни один станок не потребует внимания рабочего, равна p* = 0.9*0.8*0.85=0.612.

Тогда вероятность того, что в течении часа хотя бы один станок потребует внимания рабочего, равна P = 1 - p* = 1 - 0.612 = 0.388.

ответ: 0,388.

2. Пусть событие А состоит в том, что взятая деталь окажется бракованной.

Гипотеза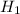 - деталь изготовлена первым автоматом.

Гипотеза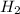 - деталь изготовлена вторым автоматом.

Вероятность события А, согласно формуле полной вероятности, равна

Найдем вероятность того, что взятая деталь бракованная изготовлена первым автоматом, по формуле Байеса, равна:

ответ: