1.один из углов, образовавшихся при пересечении двух прямых, равен 94(градусов). найдите градусные меры остальных углов. напишите с дано и с решением 2.разность смежных углов равна 42 градусам .найдите смежные углы

AC ∩ BD = O

∠AOB = 94°

∠COD, ∠AOD, ∠BOC - ?

Так как ∠AOB и ∠COD - вертикальные углы, то они равны:

∠COD = ∠AOB = 94°.  

По той же причине ∠AOD = ∠BOC. Но так как ∠AOD и ∠AOB (а также ∠BOC и ∠AOB) - смежные углы, то их сумма равна 180° (по теореме о сумме смежных углов). Отсюда следует, что:

∠AOD = ∠BOC = 180° - ∠AOB = 180° - 94° = 86°.

Задача решена!

∠COD = 94°, ∠AOD = 86° и ∠BOC = 86°.

∠AOB и ∠COB - смежные;

∠COB - ∠AOB = 42°.

∠AOB, ∠COB - ?

Пусть ∠AOB = x (x измеряем в градусах). Тогда ∠COB = x + 42°.

Так как ∠AOB и ∠COB - смежные, то их сумма равна 180°:

∠AOB + ∠COB = 180°.

Получаем следующее уравнение:

x + (x + 42°) =180°

2x + 42° = 180°

2x = 138°

x = 69°.

Значит, ∠AOB = 69°.

Тогда ∠COB = 69° + 42° = 111°.

Задача решена!

∠AOB = 69° и ∠COB = 111°.

Задача №1 : .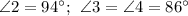

Задача №2 : .

Дано:   ;

               .

Найти:  .

------------------------------------------

, т.к. они смежные .

, т.к. они вертикальные .

, т.к. они смежные .

=============================================================

Дано:   .

Найти: .

--------------------------------------

Сумма смежных углов равна . Пусть .

************************************

Значит,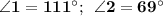 .