1. Найдите площадь поверхности сферы, если в неё можно вписать куб объёмом 64 см3
2. Площадь осевого сечения прямого кругового конуса 32см2. Радиус основания 4см. Найдите объём конуса.
Другие вопросы по теме Математика
Популярные вопросы
- Два велосипедиста начали двигаться навстречу друг другу, находящихся...
1 - У ході ізобарного стиснення гелій віддав довкіллю 6 Дж теплоти. Наскільки...
1 - Керемет жазылған .Маған көмегі тиді...
2 - Запиши в виде десятичных дробей величины, выразив их в тоннах: 9 кг,...
2 - Read the verbs and match them to the pictures make up sentences with...
2 - Назовите соединение по номенклатуре IUPAC:...
3 - решить пример по теореме Виета ( ) Можете решить? x¹= -5-√3; x²-5+√3...
1 - Поясніть функції трубчастого і пластичастого шарів з нижнього боку шапки?...
2 - Назвіть тварин, які ведуть поодинокий б життя: а)ставрида б)восьминіг...
3 - Будь ласка, до ть вирішити задачу! З погляду гача, який перебуває в потягу,...
2
1) 603.2 см²
2) 134.0 см³
Пошаговое объяснение:
1) Находим сторону квадрата:
Через сторону квадрата узнаём радиус сферы, который равен половине диагонали куба:
А через радиус по формуле выражаем площадь поверхности сферы:
2) Осевое сечение конуса - треугольник высотой с высоту конуса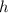 и основанием с диаметр конуса
и основанием с диаметр конуса 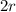 . Тогда его площадь равна
. Тогда его площадь равна 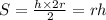
Объём конуса: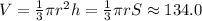 см³
см³