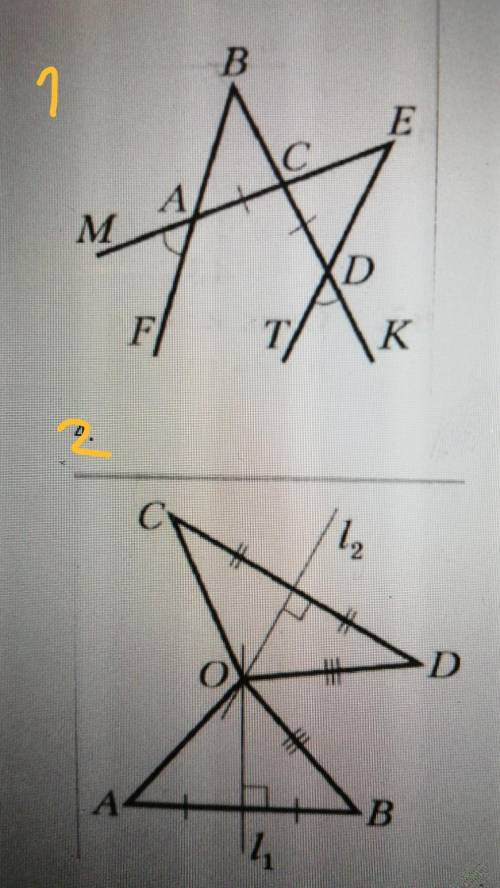
1. доказать равенство треугольников
2. доказать равенство треугольников
Другие вопросы по теме Математика
Популярные вопросы
- Филин днем плохо видит и от(того) прячется. , как )...
1 - Выразите числа 9/28 и 1 8/35 в виде приближенного значения десятичной дроби до...
2 - Согласно элементному анализу, проведенному в лаборатории, это соединение имеет...
1 - Решите уравнение: а) -5.7x=11.4 б) 0.001y=-2 в) -1.7y=-14.11 г) 3(0.4 - x)=9 д)-7/15x-3=1...
3 - 1490. товар массой в 13,3т распределили на две автомашины. на первую автомашину...
2 - Приготовлено 500 мл 18%-го (по массе) раствора сульфата меди (плотностью 1,206...
2 - Всостав планет земной группы входят: а)уран б)нептун в)солнце г)меркурий д)юпитер...
3 - Как можно написать вступление в романе, ф.достоевского преступление и наказание...
2 - Cao + c = что получается? co или co2? напишите, , полностью реакцию....
1 - Написати твiр-розповiдь осiннi берiзки...
2
Номер 1:
угол BCA= углу ECD(как вертикальные)
угол MAF= углу BAC (как вертикальные)=>
угол DTK= углу MAF=BAC=CDE
AC=CD(по усл.); BCA=ECD; BAC=CDE=>треуг. BAC= треуг.ECD по второму признаку равенства треугольников
Первый номер:
1) AC=CD - по условию
2) BAC=EDC - по свойству вертикальных углов, т.к. MAF=TDK
3) BCA=ECD - вертикальные углы
4) Треугольники BCA=ECD по стороне и прилежащим к ней углам
Что требовалось доказать.