1)cos128градусовcos52градусов-sin128градусовsin52градусов= 2)sina=12/13 ; п/2
Другие вопросы по теме Математика
Популярные вопросы
- периметр прямоугольника равен 90см,а его ширина 13см. Чему равна длина прямоугольника...
3 - 1. And / for/ of interest / related materials / amorphous alloys / applications...
3 - В группе из 48 детей соотношение мальчиков и девочек составляет 3: 5. Сколько...
3 - План до твору безсмертник?...
2 - Решите плз задачи по физике. Если сможете с полным решение...
3 - 1) В конверте среди 100 фотографий есть две, разыскиваемых. Наугад из конверта...
1 - у скринці 10 кульок, з них 4 чорні, решта-білі. Скількома можна вийняти 2...
2 - Какая связь существует между соотношением площади поверхности и объемом...
1 - с первым заданием и вторым заданием сора...
1 - Задание 1. секретный материал (ответьте на вопросы)1. что изображено2. к...
3
1) По формуле сложения сворачиваем, получается:
cos (128+52)=cos 180= -1
2) Я, так понимаю, косинус найти нужно?
Если так, то:
применяем основную тригонометрическую формулу sin^2 x+cos^2 x =1, подставляем все известные и решаем:
cos^2 x=1-(144/169)
cos^2 x=25/169
cosx = 5/13, но поскольку косинус во 2 четверти отрицательный, то ответ -5/13
3)2sin+sqrt2 = 0 (sqrt - корень)
2sin = -sqrt2
sin = -sqrt2/2
x=(-1)^k+1 *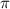 /4+2
/4+2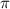 n, n
n, n  z
z
4) tg^2 x - tgx = 0
Выносим tgx за скобку:
tgx(tgx-1)=0
tgx=0 tgx-1=0
x =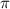 n, n
n, n  z tgx=1
z tgx=1
x=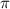 /4+
/4+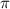 n, n
n, n  z
z