1.28 найдите и порядок каждой из подстановок
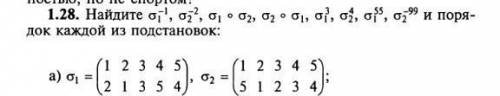
Другие вопросы по теме Математика
Популярные вопросы
- Что служит рабочим телом у двигателя паровоза?...
2 - Какие виды передач используется в велосипеде?...
3 - Чему равна амплитуда колебаний температур, если термометр показал в 7 ч. + 1оС,...
2 - Условие, при котором поршень совершает отрицательную работу...
3 - Определите суточное количество осадков, если замеры в 7 ч. показали 4 мм, в 19...
3 - В каких видах движения участвует шуруп, когда вы ввинчиваете его в доску с отвертки...
2 - В чем измеряется температура воздуха...
2 - Определите температуру воздуха за бортом самолёта, который летит на высоте 3000...
3 - Примеры тепловых двигателей...
3 - Каково назначение винта самолета...
1
На картинке показаны элементы множества A и выделены подстановки a, b, c.
1. Давайте начнем с подстановки a. Чтобы найти порядок этой подстановки, мы должны применить её последовательно снова и снова, пока не получим изначальное изображение, но при этом мы должны запоминать количество шагов, которое нам потребуется.
a = (1 3)(2 4)(5)
Давайте начнем с применения этой подстановки к числам 1, 2, 3, 4 и 5.
Применение a к 1: a(1) = 3
Применение a к 3: a(3) = 1
Таким образом, мы получаем исходное значение 1, что говорит о том, что при перестановке чисел с помощью подстановки a, мы вернулись обратно к исходному значению. Записываем это в виде a^2 = e, где e - тождественная подстановка.
Теперь посмотрим, какие значения мы получим при применении подстановки а к 2 и 4:
Применение a к 2: a(2) = 4
Применение a к 4: a(4) = 2
Таким образом, мы видим, что после двух применений подстановки a, числа 2 и 4 переходят между собой.
Следовательно, порядок подстановки а равен 2.
2. Теперь рассмотрим подстановку b:
b = (1 2 3)(4 5)
Применяя эту подстановку к числам 1, 2, 3, 4 и 5, мы получаем следующие значения:
Применение b к 1: b(1) = 2
Применение b к 2: b(2) = 3
Применение b к 3: b(3) = 1
Применение b к 4: b(4) = 5
Применение b к 5: b(5) = 4
Мы видим, что после трех применений чисел 1, 2 и 3, они возвращаются к своим исходным значениям. Также, после двух применений числа 4 и 5 меняются местами.
Следовательно, порядок подстановки b равен 3 * 2 = 6.
3. Теперь рассмотрим подстановку c:
c = (2 3)(4)
Применяя эту подстановку к числам 1, 2, 3, 4 и 5, мы получаем следующие значения:
Применение c к 1: c(1) = 1
Применение c к 2: c(2) = 3
Применение c к 3: c(3) = 2
Применение c к 4: c(4) = 4
Применение c к 5: c(5) = 5
Мы видим, что после двух применений числа 2 и 3 меняются местами. В то же время, числа 1, 4 и 5 остаются на своих местах.
Следовательно, порядок подстановки c равен 2.
Таким образом, мы нашли порядок каждой из подстановок: порядок a = 2, порядок b = 6 и порядок c = 2.