Дана гомогенная реакция 2 A2 + 4 B3 = 2 A2B + 5 B2. Равновесная концентрация вещества B2 будет равна . . . (моль/л) в момент времени, когда прореагирует 10% вещества A.
Начальные концентрации равны: С0(А2) = 2 моль/л, С0(В3) = 1,45 моль/л, С0(В2) = 0,5 моль/л.
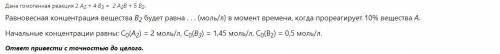
Другие вопросы по теме Химия
Популярные вопросы
- решить задачи по физике 8 класс. за ответ. Не справляюсь на до. Если то большое...
1 - Знайти загальний розв язок диференціального рівняння (9+7cos^3x)dx-cos^2xdy=0...
1 - Речь идёт о Приднестровье Как изменилось соотношение между различными группами...
2 - У сполучені посудини налили гліцерин та нафту. Обчисліть висоту нафти,якщо висота...
1 - Начертите два отрезка.пусть длина первого будет 12см а второго- одна четвертая...
1 - Брейк данс какое тело работают какие мышцы групп скажите ...
2 - Как ты думаешь почему а песне и пляске птиц царят оживления и радость...
3 - ДО 20:30 4. Какую массу серы нужно взять, чтобы в ней было столько же атомов,...
1 - Составьте предложения с приводимыми попарно словами: в дали - вдали, в начале...
2 - UOPULIUOJI UUDIUIFIOVA2ГЕОГРАФИЧЕСКОЕ ПОЛОЖЕНИЕ ЗАПАДНО - СИБИРСКОЙ РАВНИНЫ продолжить...
1
Для начала определим, сколько вещества A осталось после реакции. Поскольку прореагировало 10% вещества A, значит осталось 90% (100% - 10%) вещества A.
Концентрация вещества A2 после реакции будет равна:
С(A2) = С0(A2) - (10% * С0(A2)) = 2 моль/л - (0.1 * 2 моль/л) = 2 моль/л - 0.2 моль/л = 1.8 моль/л
Теперь определим, сколько вещества B3 прореагирует с A2. По уравнению реакции известно, что на каждые 2 моль A2 реагируют 4 моль B3. Таким образом, на каждые 1 моль A2 реагируют 2 моль B3.
Так как мы знаем, что после реакции осталось 1.8 моль A2, то количество B3, которое прореагирует с A2, будет равно:
Количество прореагировавшего B3 = 2 моль B3/моль A2 * 1.8 моль A2 = 3.6 моль B3
Теперь определим, насколько уменьшилась концентрация B3 после того, как 3.6 моль B3 прореагировало.
Исходная концентрация B3 составляла 1.45 моль/л. Теперь нужно вычесть количество прореагировавшего B3 из исходной концентрации:
Концентрация B3 после реакции = Исходная концентрация B3 - Количество прореагировавшего B3
= 1.45 моль/л - 3.6 моль/л
= -2.15 моль/л
Однако, поскольку концентрация не может быть отрицательной, то она будет равна нулю.
Таким образом, равновесная концентрация вещества B2 будет равна нулю моль/л в момент времени, когда прореагирует 10% вещества A.