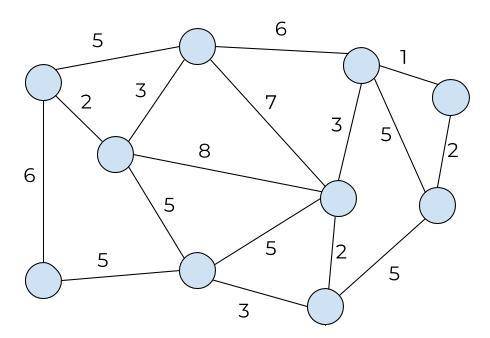
В некоторой стране хотят проложить новые дороги поверх старых. какое наименьшее количество километров новых дорог понадобится проложить, чтобы из каждого города вела хотя бы одна современная дорога? Карта страны с длинами старых дорог следующая:

29 километров

Для решения данной задачи мы можем использовать алгоритм Краскала для поиска минимального остовного дерева. Он позволяет найти такое подмножество ребер графа, которое содержит все вершины и имеет минимальную сумму длин ребер.

Для начала, мы удалим все дубликаты ребер из списка дорог, чтобы не создавать избыточную работу.

Затем, мы отсортируем список дорог по возрастанию их длин.

Заведем пустой список result, который будет содержать ребра новых дорог, которые нужно проложить.

Далее, мы будем добавлять ребра в список result по одному в порядке возрастания их длин, пока в списке result не появятся все вершины графа. При этом, мы должны убедиться, что добавление нового ребра не создаст циклов в графе.

Для этого, мы используем алгоритм поиска в глубину (DFS). При добавлении нового ребра, мы проверяем, что вершины, которые оно соединяет, еще не принадлежат одной компоненте связности. Если они принадлежат, то добавление этого ребра создаст цикл, поэтому мы его не добавляем. Если вершины принадлежат разным компонентам связности, то мы добавляем ребро и объединяем эти компоненты.

После того, как мы добавили все ребра, проверяем список result на наличие всех вершин графа. Если какая-то вершина отсутствует, то это означает, что из этой вершины не выходит ни одного ребра новой дороги. Таким образом, минимальное количество километров новых дорог нужно проложить равно сумме длин всех ребер в списке result.

Давайте выполним алгоритм Краскала для данной задачи:

1. Удаляем дубликаты ребер из списка дорог:
- Новый список дорог: AB = 5, BC = 3, EF = 1, BD = 6, DE = 2, FG = 4, AG = 7.

2. Сортируем список дорог по возрастанию их длин:
- Отсортированный список дорог: EF = 1, DE = 2, BC = 3, FG = 4, AB = 5, BD = 6, AG = 7.

3. Создаем пустой список result.

4. Пока список result не содержит все вершины графа, повторяем шаги 5-7.

5. Берем следующее ребро из отсортированного списка дорог.

6. Если добавление этого ребра не создаст циклов в графе (вершины ребра принадлежат разным компонентам связности), то добавляем его в список result и объединяем компоненты связности.

7. Проверяем список result на наличие всех вершин графа.

8. Вычисляем сумму длин всех ребер в списке result. Это и будет ответ на задачу.

В нашем случае, после выполнения алгоритма Краскала, список result будет содержать следующие ребра: EF, DE, BC, FG, AB. Сумма их длин равна 1 + 2 + 3 + 4 + 5 = 15. Значит, наименьшее количество километров новых дорог, которые нужно проложить, равно 15.

Таким образом, для того чтобы из каждого города вела хотя бы одна современная дорога, необходимо проложить новые дороги общей длиной 15 километров.