Упростите логическую функцию, покажите эквивалентность преобразованной функции исходной:
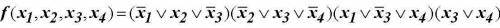
Другие вопросы по теме Информатика
Популярные вопросы
- Теплохід пройшов 58 км зі швидкістю 29км/год. скільки кілометрів за...
2 - Начерти ломаную длиной 1 дм,состоящую: 1) из трех звеньев; 2) из двух...
2 - Почему змея, крокодил, ящерица и черепаха отеносятся к одному классу....
2 - Может быть, он взял коня и помчался вскачь по лунной равнине, гонясь...
2 - Решительно из цестерны отлили 0,3 находящегося бензина. затем отлили...
1 - Мама с дочкой пекли печенье в виде звездочек сердечек и кружочков....
3 - На 118 рублей купили одинаковые пальто для мальчиков и девочек. сколько...
3 - 1. зная, что 4 x 5 и 1 y 2, оцените значение выражений: а) x + 3y...
1 - Составьте 4 предложения с оборотами there is, there are...
2 - 5предложений со словом жолда-дорога на казахском языке мне...
3
Исходная логическая функция дана в виде: F = (A + B' + C')(A' + B + C)(A + B' + C)
Для упрощения логической функции мы можем использовать логические законы и свойства алгебры логики.
1. Дистрибутивный закон
Мы можем применить дистрибутивный закон для первых двух термов (A + B' + C') и (A' + B + C):
(A + B' + C')(A' + B + C) = (A + B' + C')A' + (A + B' + C')B + (A + B' + C')C
Распишем каждое слагаемое:
(A + B' + C')A' = AA' + B'A' + C'A' = 0 + B'A' + C'A' = B'A' + C'A'
(A + B' + C')B = AB + B'B + CB = AB + 0 + CB = AB + CB
(A + B' + C')C = AC + B'C + CC = AC + B'C + 0 = AC + B'C
2. Ассоциативный закон
Мы можем применить ассоциативный закон для слагаемых, содержащих переменные A, B и C:
B'A' + C'A' = (B' + C')A'
AB + CB = (A + C)B
AC + B'C = (A + B')C
3. Коммутативный закон
Мы можем применить коммутативный закон для слагаемых, содержащих переменные A, B и C:
(B' + C')A' = A'(B' + C')
(A + C)B = B(A + C)
(A + B')C = C(A + B')
Итак, после применения всех этих законов и свойств, мы получаем упрощенную логическую функцию:
F = (B'A' + C'A')(AB + CB)(AC + B'C)
Теперь давайте проверим эквивалентность преобразованной функции и исходной, используя таблицу истинности.
Для этого нам нужно рассмотреть все возможные комбинации значений переменных A, B и C и вычислить значения F для каждой комбинации.
| A | B | C | F | (B'A' + C'A')(AB + CB)(AC + B'C) |
|---|---|---|-----------|---------------------------------|
| 0 | 0 | 0 | | |
| 0 | 0 | 1 | | |
| 0 | 1 | 0 | | |
| 0 | 1 | 1 | | |
| 1 | 0 | 0 | | |
| 1 | 0 | 1 | | |
| 1 | 1 | 0 | | |
| 1 | 1 | 1 | | |
Используя таблицу истинности, мы можем вычислить значения исходной и преобразованной функций и сравнить их, чтобы убедиться в их эквивалентности.