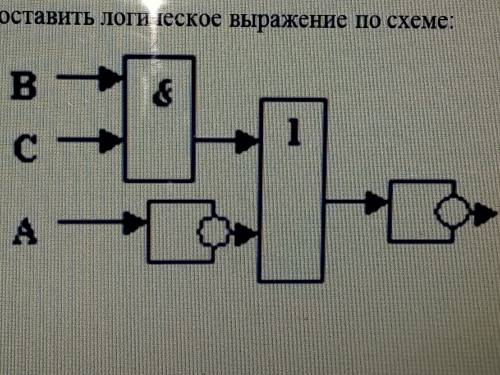
Составьте логическое выражение по схеме:

Добрый день!

Для решения данной задачи, необходимо составить логическое выражение по схеме, которая представлена на изображении.

Для начала, давайте разберемся со значениями элементов данной схемы. На изображении у нас есть следующие элементы:

- P: это предикат (условие), которое может быть истинным (true) или ложным (false).
- Q: еще один предикат (условие), которое также может быть истинным (true) или ложным (false).
- R: также предикат (условие), который может быть истинным (true) или ложным (false).
- И: обозначает операцию "и" (AND), которая возвращает true только в случае, если оба предиката, которые соединены этим оператором, истинны.
- ИЛИ: обозначает операцию "или" (OR), которая возвращает true, если хотя бы один из предикатов, которые соединены этим оператором, истинен.
- НЕ: обозначает операцию "не" (NOT), которая меняет истинные предикаты на ложные и наоборот.

С учетом данных элементов, можем перейти к составлению логического выражения.

Сначала посмотрим на первую строку с элементами P и Q, которые соединены операцией "не" (NOT). Это означает, что нам нужно инвертировать значения предикатов P и Q.

После инвертирования, получим следующие значения:

- Неверно (not true) = false (ложь)
- Верно (not false) = true (истина)

Теперь перейдем ко второй строке с элементами R и P.

У нас присутствует операция "и" (AND), что означает, что выходное значение будет истинным (true) только тогда, когда оба входных предиката также являются истинными (true).

Таким образом, получим следующие значения:

- Истина (true) и Ложь (false) = Ложь (false)
- Истина (true) и Истина (true) = Истина (true)
- Ложь (false) и Ложь (false) = Ложь (false)
- Ложь (false) и Истина (true) = Ложь (false)

Наконец, перейдем к третьей строке, где присутствует операция "или" (OR), что означает, что выходное значение будет истинным (true), если хотя бы один из входных предикатов также является истинным (true).

Получим следующие значения:

- Ложь (false) или Истина (true) = Истина (true)
- Истина (true) или Ложь (false) = Истина (true)
- Ложь (false) или Ложь (false) = Ложь (false)
- Истина (true) или Истина (true) = Истина (true)

Итак, полученное логическое выражение по схеме будет: (¬P∧Q)∨(R∧P).

В этом выражении:
¬ - обозначение отрицания (NOT)
∧ - обозначение операции "и" (AND)
∨ - обозначение операции "или" (OR)

Надеюсь, что мой ответ понятен и полезен. Если у вас возникнут еще вопросы, не стесняйтесь задавать.'