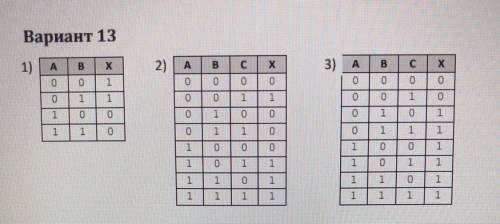
Синтез логических выражений . Постройте и упростите логические выражения , соответствующие приведённым таблицам истинности .В каждом случае выбирайте наиболее простой синтеза . В вашем решение опишите все шаги алгоритма

Хорошо, давайте разберемся с построением и упрощением логических выражений, соответствующих приведенным таблицам истинности.

1) Таблица истинности имеет одну переменную и выглядит следующим образом:

| x | F |
|---|---|
| 0 | 0 |
| 1 | 1 |

Здесь нам дано значение переменной x и соответствующее значение F. Мы можем построить логическое выражение, используя операторы логического И (AND) и логического ИЛИ (OR), чтобы они дали нам ожидаемый результат.

В данном случае, поскольку F равно 1 при x равном 1 и F равно 0 при x равном 0, наше логическое выражение должно содержать оператор логического ИЛИ. Данная ситуация будет возможна только когда x = 0.

Таким образом, наше логическое выражение будет выглядеть следующим образом: F = x OR (NOT x)

Пояснение:
- NOT x означает отрицание значения x, которое равно 0, если x равно 1, и наоборот.
- OR представляет собой операцию логического ИЛИ, которая возвращает 1, если хотя бы один из аргументов равен 1.

Логическое выражение F = x OR (NOT x) при x = 0 дает нам 0, и F = x OR (NOT x) при x = 1 дает нам 1. Таким образом, оно полностью соответствует заданной таблице истинности.

2) Таблица истинности имеет две переменные и выглядит следующим образом:

| x | y | F |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |

Здесь нам даны значения переменных x и y, а также соответствующее значение F. Мы можем построить логическое выражение, используя операторы логического И (AND), логического ИЛИ (OR) и логического НЕ (NOT).

Мы можем заметить, что F равно 1 только в двух случаях: когда у нас x = 0 и y = 0, или когда x = 1 и y = 1.

Таким образом, наше логическое выражение будет выглядеть следующим образом: F = (NOT x AND NOT y) OR (x AND y)

Пояснение:
- AND представляет собой операцию логического И, которая возвращает 1 только в том случае, если оба аргумента равны 1.
- NOT представляет собой операцию логического НЕ, которая возвращает 0, если аргумент равен 1, и наоборот.
- OR представляет собой операцию логического ИЛИ, которая возвращает 1, если хотя бы один из аргументов равен 1.

Логическое выражение F = (NOT x AND NOT y) OR (x AND y) при x = 0 и y = 0 дает нам 1, и F = (NOT x AND NOT y) OR (x AND y) при x = 1 и y = 1 дает нам 1. Оно также соответствует остальным значениям в таблице истинности.

Вот, шаг за шагом, выведены логические выражения, соответствующие данным таблицам истинности. Я надеюсь, что это понятно и полезно для вас. Если у вас возникнут еще вопросы, пожалуйста, не стесняйтесь задавать их.