Решите задачи 1. В цветовой модели RGB для кодирования одного пикселя используется 3
байта. Фотографию размером 2048x1536 пикселей сохранили в виде
несжатого файла с использованием RGB-кодирования. Определите размер
получившегося файла.
2. Для хранения растрового изображения размером 128*128 пикселей отвели
4 килобайта памяти. Каково максимально возможное число цветов в палитре
изображения?
3. Укажите минимальный объем памяти (в килобайтах), достаточный для
хранения любого растрового изображения размером 64*64 пикселя, если
известно, что в изображении используется палитра из 256 цветов. Саму
палитру хранить не нужно.
4. Для хранения растрового изображения размером 64*64 пикселя отвели 512
байтов памяти. Каково максимально возможное число цветов в палитре
изображения?

0.

w*h = 2048x1536 px

i = 3 байта

V = 2048 * 1536 * 3 = 9437184 байта = 9216 Кбайт = 9 Мбайт

1.

128 * 128 = 16384 px

4 Кб = 32768 бит

32768 / 16384 = 2 бита на пиксель

= 4

2.

K = 64 * 64 = 4096

i = 8

4096 * 8 = 32768 бит = 4 Кбайт

3.

K = 64*64 = 4096 px

V = 512 байт = 4096 бит

i = V/K = 1

N =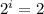

Объяснение:

Давайте решим эти задачи по очереди.

1. В цветовой модели RGB каждый пиксель кодируется с помощью 3 байтов, что составляет 24 бита (поскольку 1 байт равен 8 битам).
Таким образом, для каждого пикселя необходимо 24 бита памяти.

У нас есть фотография размером 2048x1536 пикселей. Для определения размера файла, необходимо умножить количество пикселей на количество битов:

2048 x 1536 x 24 = 748,683,264 бит

Теперь, чтобы получить размер файла в байтах, нужно разделить полученную сумму на 8, так как 1 байт равен 8 битам:

748,683,264 / 8 = 93,585,408 байт

Таким образом, получившийся файл будет иметь размер 93,585,408 байт.

2. Для хранения растрового изображения размером 128x128 пикселей отведено 4 килобайта памяти. Мы хотим определить максимально возможное число цветов в палитре изображения.

Память, отведенная для хранения изображения, составляет 4 килобайта, что равно 4,096 байтам.
В данном случае, каждый пиксель будет кодироваться с помощью одного байта, поскольку количество цветов в палитре ограничено.

Таким образом, максимально возможное число цветов в палитре изображения будет равно 4,096 (количество байт, отведенных для памяти).

3. Для определения минимального объема памяти (в килобайтах), необходимого для хранения любого растрового изображения размером 64x64 пикселя, при известной палитре из 256 цветов, мы можем использовать следующую формулу:

Объем памяти (в битах) = количество пикселей x количество бит на каждый пиксель = 64 x 64 x log2(256)

Мы используем log2(256), поскольку каждый пиксель будет кодироваться с помощью 8 бит (так как имеется 256 цветов в палитре, и для их кодирования требуется 8 бит).

Объем памяти (в битах) = 64 x 64 x log2(256) = 64 x 64 x 8 = 32,768 бит.

Теперь, чтобы получить размер памяти в килобайтах, необходимо разделить полученную сумму на 8,192 (поскольку 1 килобайт равен 8,192 битам):

32,768 / 8,192 = 4 килобайта.

Таким образом, минимальный объем памяти, достаточный для хранения любого растрового изображения размером 64x64 пикселя с использованием палитры из 256 цветов, составляет 4 килобайта.

4. Для хранения растрового изображения размером 64x64 пикселя отведено 512 байтов памяти. Мы хотим определить максимально возможное число цветов в палитре изображения.

В этом случае, каждый пиксель будет кодироваться с помощью ограниченного числа битов, поскольку размер памяти ограничен.

Объем памяти (в битах) = количество пикселей x количество бит на каждый пиксель = 64 x 64 x log2(N)

Теперь мы можем решить это уравнение, чтобы найти максимально возможное число цветов в палитре изображения (N):

64 x 64 x log2(N) = 512

Для упрощения вычислений, давайте заменим log2(N) на x:

64 x 64 x x = 512

64 x 64 = 4,096

4,096 x x = 512

x = 512 / 4,096 = 0.125

Теперь, чтобы получить максимально возможное число цветов в палитре изображения, мы должны вернуться к уравнению и заменить x на log2(N):

log2(N) = 0.125

2^0.125 = N

N = 2^(0.125) = 1.112

Максимально возможное число цветов в палитре изображения составит около 1.112. Однако, поскольку цветовое кодирование обычно имеет ограничение на целые числа, в нашем случае будет доступно 2 цвета в палитре изображения.