Решите уравнение 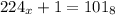. Напишите результат вычислений в троичной системе счисления.

12

Объяснение:

Чтобы решить уравнение применим развернутую запись чисел (сумму цифр числа умноженных на основание системы счисления в степени разряда)

2 * х² + 2 * х¹ + 4 * х⁰ + 1 = 1 * 8² + 0 * 8¹ + 1 * 8⁰

2 * х² + 2 * х + 4 * 1 + 1 = 1 * 64 + 0 * 8 + 1 * 1

2х² + 2х + 4 + 1 = 64 + 0 + 1

2х² + 2х + 5 = 65

2х² + 2х + 5 - 65 = 0

2х² + 2х - 60 = 0

Теперь решим обычное квадратное уравнение:

2х² + 2х - 60 = 0

D = b² - 4ac

D = 2² - 4 * 2 * (-60) = 4 - 8 * (-60) = 4 + 480 = 484

Второй х можно не рассматривать, т.к. он будет отрицательным

Сделаем проверку в 10 СС:

224₅ = 2 * 5² + 2 * 5¹ + 4 * 5⁰ = 2 * 25 + 2 * 5 + 4 * 1 = 50 + 10 + 4 = 64

101₈ = 1 * 8² + 0 * 8¹ + 1 * 8⁰ = 1 * 64 + 0 * 8 + 1 * 1 = 64 + 0 + 1 = 65

64 + 1 = 65

Переведём результат в 3 СС:

5 / 3 = 1 + остаток 2

1 / 3 = 0 + остаток 1

записываем остатки снизу вверх

5₁₀= 12₃