Определите минимальное основание системы счисления, чтобы при записи числа 21 последним символом был 0. Если возможно объяснить решение(можно и кратко)

Ответы

liq2354234 15.10.2020 15:23

(см. объяснение)

Объяснение:

Число 21 в развернутой форме записи можно представить так:

$21_{10}=a\times n^k+b\times n^{k-1}+...+c\times n^{1}+d\times n^0$

Из условия задачи следует, что последнее число в системе счисления с основанием n равно 0, т.е.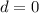 d=0 .

Тогда получим:

$21_{10}=a\times n^k+b\times n^{k-1}+...+c\times n^{1}$

Заметим, что n можно вынести за скобки:

$21_{10}=n(a\times n^{k-1}+b\times n^{k-2}+...+c)$

Разделим обе части равенства на n:

$\dfrac{21}{n}=a\times n^{k-1}+b\times n^{k-2}+...+c$

Получили, что 21 делится на основание системы счисления без остатка.

Учитывая, что n>1, наименьший делитель числа 21 - это 3.

Поэтому минимальное основание системы счисления, при записи числа 21 в которой последним символом будет 0 равно 3.

И действительно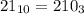 $21_{10}=210_3$ .

Задача решена!

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Информатика

10ok 15.06.2019 19:20

Aleks0528 15.06.2019 19:20

irinaa10 15.05.2020 11:30

Ангелиныч1 15.05.2020 11:30

tseng7788 15.05.2020 11:30

koblovalv 15.05.2020 11:30

yanaskazka777 30.01.2021 19:21

юлд1 18.05.2021 08:36

liudmilka19091982 28.06.2019 16:08

Shiro1303 28.06.2019 15:45