некоторый алфавит содержит 107 символов. Сообщение содержит 15 символов. Определите информац. обьем сообщения в битах

Ответы

Walker95 31.01.2022 01:00

Дано:

$$\mbox{\mathversion{bold} \displaystyle N=107}$ символов (мощность (размер) алфавита)

$$\mbox{\mathversion{bold} \displaystyle K=15 }$ символов (длина сообщения)

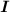Найти: $$\mbox{\mathversion{bold} \displaystyle I }$ (информац.объём сообщения, кол-во информации в нём)

Находим количество информации в одном символе.

По сути, это минимальное количество двоичных разрядов, в котором можно хранить один символ нашего алфавита.

Выбирается оно из таблицы степеней двойки (первое значение, не меньшее, чем наше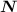 $$\mbox{\mathversion{bold} \displaystyle N }$ ), либо через формулу 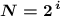$$\mbox{\mathversion{bold} \displaystyle N=2^{\,i} }$ (подбирая минимальное подходящее 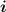$$\mbox{\mathversion{bold} \displaystyle i }$ , либо решая уравнение через нахождение двоичного логарифма и затем округляя всегда с избытком, вверх).

Пример подбора:

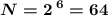если $$\mbox{\mathversion{bold} \displaystyle i=6 }$ , то $$\mbox{\mathversion{bold} \displaystyle N=2^{\,6}=64 }$ (алфавит из 64 символов можно хранить; для нас мало, надо минимум 107)

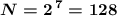если $$\mbox{\mathversion{bold} \displaystyle i=7 }$ , то $$\mbox{\mathversion{bold} \displaystyle N=2^{\,7}=128 }$ (алфавит из 128 символов можно хранить; для нас достаточно, это даже больше, чем наши 107 символов в алфавите)

Выбираем минимальную подходящую степень= 7 (т.е. $$\mbox{\mathversion{bold} \displaystyle i=7 }$ бит)

Пример расчёта:

$$\mbox{\mathversion{bold} \displaystyle N=2^{\,i} }$

$$\mbox{\mathversion{bold} \displaystyle 107=2^{\,i} }$

отсюда, получаем что:

$$\mbox{\mathversion{bold} \displaystyle i=\log_2 107=\frac{\lg 107}{\lg 2}=\frac{\ln 107}{\ln 2}=6{,}741... }$

Можно считать одним из трёх : считать сам двоичный логарифм (если логарифм по произвольному основанию есть в вашем калькуляторе- во встроенном в Windows 10, в инженерном виде он есть например), или можно считать отношение десятичных либо натуральных логарифмов (см. дроби в расчёте). Десятичные либо натуральные логарифмы обычно есть в научных калькуляторах.

Получилось дробное значение, значит округляем до целого, но не как обычно, а всегда вверх (то есть, всегда берём целое число, большее чем наш результат). Так округляем потому, что нам нужно получить возможность хранить чуть больше символов, чем есть в нашем алфавите (раз уж ровно 107 не выходит).

Получаем, что: $$\mbox{\mathversion{bold} \displaystyle i=7 }$ бит

Далее, находим информационный объём сообщения:

$$\mbox{\mathversion{bold} \displaystyle I=K\cdot i=15\cdot 7=105 }$ бит