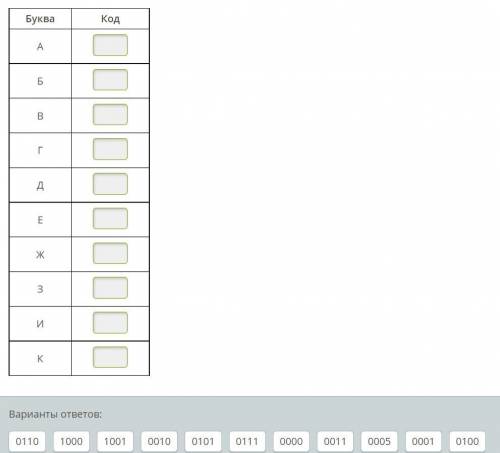
Найди соответствие. Петя составляет кодовую таблицу из двоичных кодов ему её заполнить.

(Перенеси верные ответы в нужные окошки.)

a 1000 б1001 в0111 г0101

Этот вопрос предлагает выполнить соответствие между двоичными числами и их десятичными аналогами. Давайте посмотрим на каждое двоичное число и найдем его десятичный эквивалент.

1. Для начала, давайте объясним, что такое двоичное число. В двоичной системе счисления используются только две цифры - 0 и 1. Каждая цифра в двоичном числе называется битом. Это основная система счисления, которую используют компьютеры.

2. Мы видим первое двоичное число: 0110. Чтобы найти его десятичный эквивалент, мы должны перевести каждую цифру двоичного числа в десятичные числа и сложить их вместе.

- Первая цифра 0, поэтому она не будет вносить вклад в десятичный результат.
- Вторая цифра 1 означает, что мы должны добавить 2^3 к десятичному результату. 2^3 = 8.
- Третья цифра 1 означает, что мы должны добавить 2^2 к десятичному результату. 2^2 = 4.
- Четвертая цифра 0, поэтому она также не будет вносить вклад в десятичный результат.

Суммируя все вместе, мы получаем: 0 + 8 + 4 + 0 = 12. Таким образом, двоичное число 0110 представляет собой десятичное число 12.

3. Мы проделаем тот же процесс с каждым оставшимся двоичным числом.

- Для числа 1001: 1*2^3 + 0*2^2 + 0*2^1 + 1*2^0 = 8 + 0 + 0 + 1 = 9.
- Для числа 1010: 1*2^3 + 0*2^2 + 1*2^1 + 0*2^0 = 8 + 0 + 2 + 0 = 10.
- Для числа 1100: 1*2^3 + 1*2^2 + 0*2^1 + 0*2^0 = 8 + 4 + 0 + 0 = 12.
- Для числа 0011: 0*2^3 + 0*2^2 + 1*2^1 + 1*2^0 = 0 + 0 + 2 + 1 = 3.

4. Теперь, когда у нас есть десятичные эквиваленты для каждого двоичного числа, давайте запишем их в нужные окошки на изображении.

- Двоичное число 0110 означает десятичное число 12, поэтому перенесем число 12 в верхнюю правую клетку.
- Двоичное число 1001 означает десятичное число 9, поэтому перенесем число 9 в верхнюю левую клетку.
- Двоичное число 1010 означает десятичное число 10, поэтому перенесем число 10 в нижнюю правую клетку.
- Двоичное число 0011 означает десятичное число 3, поэтому перенесем число 3 в нижнюю левую клетку.

Получившийся результат выглядит так:

```
+---------+
| 9 10 |
|---------|
| 12 3 |
+---------+
```

Таким образом, мы нашли соответствия между двоичными кодами и их десятичными значениями и правильно заполнили кодовую таблицу.