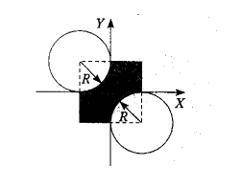
Написать программу на языке С++, которая определяет, попадает ли точка с заданными координатами x и y в область, закрашенную на рисунке чёрным цветом. Результат работы программы вывести в виде текстового сообщения на экран.
Другие вопросы по теме Информатика
Популярные вопросы
- во к произведению Гулливер в стране лилипутов Автор: Джонатан Свифт. ...
1 - ІІІ рівень. Дати фізико-географічну характеристику степової зони використовуючи...
3 - заранее с вираз і знайдіть його значення 0,5(1,6x-6,4y)-2,4(1,5x+y)якщо,...
3 - Скільки вітсотків поїздок здійснються з метою розваг і відпочинку у міжнародному...
1 - с геометрией. Задания на фотоПункты б) в) ...
1 - 1) Скільки разів буде виконано такий цикл? for i := 5 downto 1 do 2)Який...
2 - Чи залежить концентрація іонів в електроліті від сили струму, що проходить...
1 - Клітинна інженерія.Які моральні і соціальні аспекти можуть мати місце...
1 - У розчині міститься 36% солі. Якщо додати 130 г солі, то в розчині буде...
1 - Составьте трассировочную таблицу по заданию ниже: (ЭТО ОЧЕНЬ...
3
Для начала, давайте определим границы этой области. На рисунке видно, что область закрашена тремя частями:
1. Прямоугольник с границами (x1, y1) и (x2, y2).
2. Круг с центром в точке (cx, cy) и радиусом r.
3. Треугольник с вершинами (tx1, ty1), (tx2, ty2) и (tx3, ty3).
Теперь, чтобы определить, попадает ли точка в эту область, мы должны проверить выполняются ли условия каждой из составляющих области фигур.
Для вычисления, попадает ли точка внутрь прямоугольника, нам нужно убедиться, что x находится в диапазоне от x1 до x2, а y находится в диапазоне от y1 до y2:
```
if (x >= x1 && x <= x2 && y >= y1 && y <= y2) {
// точка находится внутри прямоугольника
}
```
Для вычисления, попадает ли точка внутрь круга, мы должны использовать уравнение окружности и проверить, что расстояние между точкой (x, y) и центром круга (cx, cy) не превышает радиус r:
```
if (((x - cx) * (x - cx) + (y - cy) * (y - cy)) <= (r * r)) {
// точка находится внутри круга
}
```
Для вычисления, попадает ли точка внутрь треугольника, мы можем воспользоваться формулой, называемой "Треугольник Пуанкаре" или "Шерроу" (Shoelace formula), которая основывается на координатах вершин треугольника. Формула имеет следующий вид:
```
area = 0.5 * abs((tx1 * (ty2 - ty3) + tx2 * (ty3 - ty1) + tx3 * (ty1 - ty2)));
triangleArea = 0.5 * (abs((tx1 * (ty2 - y) + tx2 * (y - ty1) + x * (ty1 - ty2)) +
abs((tx1 * (y - ty3) + x * (ty3 - ty1) + tx3 * (ty1 - y))) +
abs((x * (ty2 - ty3) + tx2 * (ty3 - y) + tx3 * (y - ty2)))));
if (triangleArea == area) {
// точка находится внутри треугольника
}
```
Если точка попадает хотя бы в одну из вышеописанных фигур, то можно выводить текстовое сообщение на экран, что точка находится внутри области. Если ни одно из условий не выполнено, то точка находится вне области.
Полный код программы на языке С++:
```cpp
#include
#include
using namespace std;
int main() {
double x, y;
// Введите координаты точки
cout << "Введите x: ";
cin >> x;
cout << "Введите y: ";
cin >> y;
// Задаем границы для каждой фигуры
double x1 = -4, y1 = 4, x2 = 4, y2 = 2; // прямоугольник
double cx = 0, cy = 0, r = 3; // круг
double tx1 = -2, ty1 = 2, tx2 = 2, ty2 = 2, tx3 = 0, ty3 = -3; // треугольник
// Проверяем, попадает ли точка в область
if (x >= x1 && x <= x2 && y >= y1 && y <= y2) {
cout << "Точка находится внутри прямоугольника" << endl;
} else if (((x - cx) * (x - cx) + (y - cy) * (y - cy)) <= (r * r)) {
cout << "Точка находится внутри круга" << endl;
} else {
double area = 0.5 * abs((tx1 * (ty2 - ty3) + tx2 * (ty3 - ty1) + tx3 * (ty1 - ty2)));
double triangleArea = 0.5 * (abs((tx1 * (ty2 - y) + tx2 * (y - ty1) + x * (ty1 - ty2))) +
abs((tx1 * (y - ty3) + x * (ty3 - ty1) + tx3 * (ty1 - y))) +
abs((x * (ty2 - ty3) + tx2 * (ty3 - y) + tx3 * (y - ty2))));
if (triangleArea == area) {
cout << "Точка находится внутри треугольника" << endl;
} else {
cout << "Точка находится вне области" << endl;
}
}
return 0;
}
```
После запуска данной программы, она будет запрашивать у пользователя ввести координаты точки (x и y) и выводить соответствующее сообщение о принадлежности точки к заданной области.