написать программу (на Паскале)которая определяет лежит ли точка а внутри треугольной области 2x+y=4 (внутри понимается в строгом смысле, то есть случай, когда А лежит на границе области-недопустим
Ответы
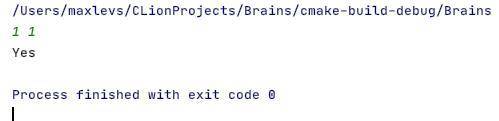
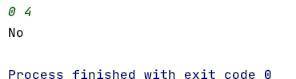
Код#include <iostream>#include <cmath>#include <exception>class Point;class Figure;class Circle;class Rectangle;class UnitedFigure;class ComplementedFigure;class IntersectedFigure;template <typename T>int sign(T number) { if (number > 0) return 1; if (number == 0) return 0; return -1;}class Point {public: double x; double y; Point() = default; Point(double x, double y) : x(x), y(y) {} Point operator + (const Point& p) const { return Point {x + p.x, y + p.y}; } Point operator - (const Point& p) const { return Point {x - p.x, y - p.y}; } double operator * (const Point& p) const { return Point::dot(*this, p); } Point operator * (double k) const { return Point { k * x, k * y }; } static Point max (const Point& p1, const Point& p2) { return Point {std::max(p1.x, p2.x), std::max(p1.y, p2.y)}; } static Point min (const Point& p1, const Point& p2) { return Point {std::min(p1.x, p2.x), std::min(p1.y, p2.y)}; } static double dot (const Point& p1, const Point& p2) { return p1.x * p2.x + p1.y + p2.y; } template<typename T> static T clamp (const T& p, const T& min, const T& max) { if (p >= min and p <= max) { return p; } if (p < min) { return min; } if (p > max) { return max; } throw std::runtime_error("How have you could take this like??"); } double vec_length () const { return sqrt(x*x + y*y); }};class Figure {public: [[nodiscard]] virtual double distance_to (const Point &p) const = 0; friend UnitedFigure operator + (const Figure & f1, const Figure & f2); friend ComplementedFigure operator - (const Figure & f1, const Figure & f2); friend IntersectedFigure operator & (const Figure & f1, const Figure & f2); bool is_point_into(const Point &p) const { return distance_to(p) <= 0; } bool is_point_strict_into(const Point &p) const { return distance_to(p) < 0; }};class Circle : public Figure { Point o; double r;public: Circle (Point p, double r) : o(p), r(r) {} [[nodiscard]] double distance_to (const Point &p) const override { return (o - p).vec_length() - r; }};class Rectangle : public Figure { Point a; Point b;public: Rectangle (Point p1, Point p2) : a(Point::min(p1, p2)), b(Point::max(p1, p2)) {} [[nodiscard]] double distance_to (const Point &p) const override { auto d = Point::max(a - p, p - b); return Point::max(d, Point {0, 0}).vec_length() + std::min(0.0, std::max(d.x, d.y)); }};class Triangle : public Figure { Point a; Point b; Point c;public: Triangle(const Point &a, const Point &b, const Point &c) : a(a), b(b), c(c) { } [[nodiscard]] double distance_to(const Point &p) const override { auto p0 = a, p1 = b, p2 = c; auto e0 = p1 - p0; auto e1 = p2 - p1; auto e2 = p0 - p2; auto v0 = p - p0; auto v1 = p - p1; auto v2 = p - p2; auto pq0 = v0 - e0*Point::clamp( Point::dot(v0,e0)/Point::dot(e0,e0), 0.0, 1.0 ); auto pq1 = v1 - e1*Point::clamp( Point::dot(v1,e1)/Point::dot(e1,e1), 0.0, 1.0 ); auto pq2 = v2 - e2*Point::clamp( Point::dot(v2,e2)/Point::dot(e2,e2), 0.0, 1.0 ); double s = sign( e0.x * e2.y - e0.y * e2.x ); auto d = Point::min(Point::min( Point {Point::dot(pq0,pq0), s*(v0.x*e0.y-v0.y*e0.x)}, Point {Point::dot(pq1,pq1), s*(v1.x*e1.y-v1.y*e1.x)}), Point {Point::dot(pq2,pq2), s*(v2.x*e2.y-v2.y*e2.x)}); auto r = -sqrt(-d.x)*sign(d.y); // debug this later return r; }};class UnitedFigure : public Figure { const Figure &f1; const Figure &f2;public: UnitedFigure (const Figure &_f1, const Figure &_f2) : f1(_f1), f2(_f2) {} [[nodiscard]] double distance_to(const Point &p) const override { return std::min(f1.distance_to(p), f2.distance_to(p)); }};class ComplementedFigure : public Figure { const Figure &f1; const Figure &f2;public: ComplementedFigure (const Figure &_f1, const Figure &_f2) : f1(_f1), f2(_f2) {} [[nodiscard]] double distance_to(const Point &p) const override { return std::max(f1.distance_to(p), -f2.distance_to(p)); }};class IntersectedFigure : public Figure { const Figure &f1; const Figure &f2;public: IntersectedFigure (const Figure &_f1, const Figure &_f2) : f1(_f1), f2(_f2) {} [[nodiscard]] double distance_to(const Point &p) const override { return std::max(f1.distance_to(p), f2.distance_to(p)); }};UnitedFigure operator + (const Figure & f1, const Figure & f2) { return UnitedFigure{f1, f2};}ComplementedFigure operator - (const Figure & f1, const Figure & f2) { return ComplementedFigure{f1, f2};}IntersectedFigure operator & (const Figure & f1, const Figure & f2) { return IntersectedFigure{f1, f2};}int main() { Point A {}; std::cin >> A.x >> A.y; Triangle figure(Point{0, 0}, Point{2, 0}, Point{0, 4}); std::cout << (figure.is_point_strict_into(A) ? "Yes" : "No") << std::endl; return 0;}


ПОКАЗАТЬ ОТВЕТЫ




Другие вопросы по теме Информатика
Популярные вопросы
- Однородное магнитное поле, индукция которого 0,5 тл, действует с силой 5н на...
3 - 1. почему именно пожилые люди дальнозоркостью? 2. что происходит со слухом, если...
1 - 10 (8 )прочитайте фрагмент текста и переведите его на современный язык.дайте...
3 - Можете рассказать чем занимались девушку из повести а зори здесь тихии до войны...
3 - Подчеркнуть подлежащее и сказуемое в предложениях и расставить тире там где его...
2 - ответить на 7 вопросов по информатике 4 класс...
2 - Написать обозначения словам ветеран и дектатор это ! 15...
3 - Папа пошел в магазин. на первую покупку он истратил 3/4 всех своих денег и еще...
3 - Складіть таблицю у зошиті «ічні відкриття кінця 15 століття першої половини 16...
2 - Вставь буквы в окончания глаголов 3 лица множественного числа отметь вариант...
3