Ханойская башня на Python 3. Ввод: Первая строка содержит количество дисков - натуральное число N (N≤10^5). Вторая строка файла содержит строку символов длины N. Для каждого i (1≤i≤N) i-й символ - 'A', если диск с номером i находится на стержне A, 'B' - если на стержне B, 'C' - если на стержне C.
Вывод: В единственной строке должно быть выведено одно неотрицательное число - минимальное количество оборотов, необходимое для того, чтобы все диски располагались на стержне B, согласно модулю 10^9 + 9. Последнее условие не имеет другого смысла, кроме уменьшения размера выходного числа.

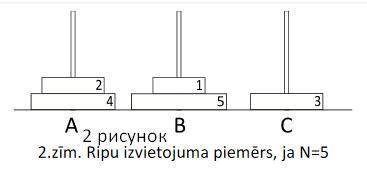
Например, если пять дисков расположены, как показано на рисунке 2, то требуется 10 ходов, чтобы расположить их на стержне B: A → C, B → C, A → B, C → B, C → A, B → A, C → B, A → C, A → B, C → B. Чтобы упростить задачу, на этот раз вам нужно будет найти только наименьшее количество необходимых ходов. Напишите программу, определяющую минимально необходимое количество оборотов после модуля 10 ^ 9 + 9 для данной колесной формулы, чтобы все колеса были помещены на стержень B.

оалклклкл    2   18.12.2020 19:03    1