Этот класс задач связан с выбором конкретных вариантов органи-зации системы с учетом ресурсных ограничений. Как правило, в зада-чах логического выбора используются изменяемые ячейки, которые могут хранить одно из двух значений: 1 или 0, - иначе «выбирать ва-риант организации» или «не выбирать». В математическом програм-мировании такие задачи называются задачами булевского програм-мирования. Использование булевских переменных позволяет сформулировать различные логические ограничения выбора.

Например, выбор одного из 2-х вариантов организации исследуе-мой системы (1,2) может определяться двумя булевскими переменны-ми (Х1, Х2).

Условие выбора только одного из двух вариантов эквивалентно логическому ограничению: Х1+Х2=1. Такое ограничение моделирует условие взаимоисключения.

Условие выбора хотя бы одного из двух вариантов эквивалентно логическому ограничению Х1+Х2>=1.

Если вариант 2 может быть принят только при принятии варианта 1 (взаимообусловленность) следует использовать ограничение Х1>=Х2. Если же вариант 2 должен быть принят при принятии вари-анта 1, вводится ограничение Х2>=Х1.

В качестве примера рассмотрим задачу о выборе варианта капита-ловложений.

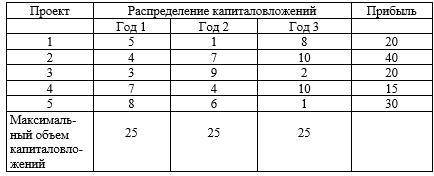
Распределение капиталовложений

Проект Распределение капиталовложений Прибыль

Год 1 Год 2 Год 3

1 5 1 8 20

2 4 7 10 40

3 3 9 2 20

4 7 4 10 15

5 8 6 1 30

Максималь-ный объем капиталовло-жений 25 25 25

Рассматриваются пять проектов, которые могут быть осуществле-ны в течение последующих трех лет. Ожидаемые величины прибыли от реализации каждого из проектов и распределение необходимых капиталовложений по годам (в тыс.$.) приведены в таблице. Предпо-лагается, что каждый утвержденный проект будет реализован за трех-летний период. Требуется выбрать совокупность проектов, которой соответствует максимум суммарной прибыли.

Добавим к таблице исходных данных столбец изменяемых ячеек. Обозначим содержимое этих ячеек как Xi, где i=1, 2,..., 5 определяет номер проекта, а Xi определяет решение: вкладывать (Xi=1) или нет (Xi=0) средства в i-ый проект. Такую переменную, принимающую только два возможных значения (1 или 0), называют булевской.

Ограничения:

1) по объему капиталовложений

в первый год: 5* X1 + 4*X2 +3*X3 + 7*X4 + 8*X5 <= 25;

во второй год: 1* X1 + 7*X2 +9*X3 + 4*X4 + 6*X5 <= 25;

в третий год: 8* X1 + 10*X2 +2*X3 + 10*X4 + 1*X5 <= 25;

2) “естественные” ограничения:

X1X5 = двоичные (булевские)

Целевая функция:

Z= 20*X1 + 40*X2 + 20*X3 + 15*X4 + 30*X5;

Максимизировать Z.

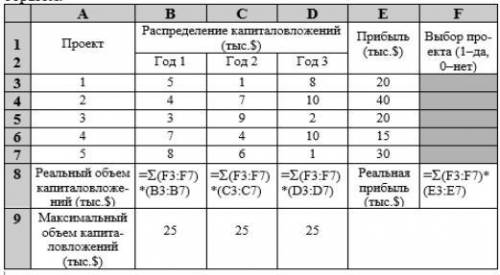
Электронная таблица в этом варианте может выглядеть следую-щим образом.

A B C D E F

1 Проект Распределение капиталовложений (тыс.$) Прибыль (тыс.$) Выбор про-екта (1–да, 0–нет)

2 Год 1 Год 2 Год 3

3 1 5 1 8 20

4 2 4 7 10 40

5 3 3 9 2 20

6 4 7 4 10 15

7 5 8 6 1 30

8 Реальный объем капиталовложе-ний (тыс.$) =(F3:F7)*(B3:B7) =(F3:F7)*(C3:C7) =(F3:F7)*(D3:D7) Реальная прибыль (тыс.$) =(F3:F7)*(E3:E7)

9 Максимальный объем капита-ловложений (тыс.$) 25 25 25

Формула =(F3:F7)*(B3:B7) записывается в системе EXCEL как СУММПРОИЗВ (F3:F7;B3:B7), она определяет сумму произведений столбца F3:F7 на столбец B3:B7:

Если Excel не видит формулы, то расписываем вручную, следую-щим образом: СУММПРОИЗВ (F3:F7;B3:B7) = F3*B3 + F4*B4 + F5*B5 + F6*B6 + F7*B7.

F3:F7 – изменяемые булевские ячейки, F8 – целевая ячейка, огра-ничения: B8:D8<=B9:D9, F3:F7 - двоичные

ЛизаНагайцева03    3   26.05.2021 16:55    3