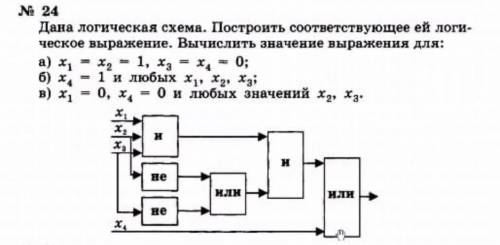
Дана логическая схема. Построить логическое выражение, соответствующее этой схеме. Вычислить значение выражения для А) х1= х 2 =1, х 3= х 4 =0 Б) х 4 =1, и любых значениях х1, х2, х3 В) х 1 =0, х 4 =0 и любых значениях х 2, х 3.

Хорошо, давайте разберемся с этой логической схемой.

Данная схема представляет собой комбинационную логическую схему, состоящую из логических элементов "И" ("AND"), "ИЛИ" ("OR") и "НЕ" ("NOT").

Для построения логического выражения, соответствующего данной схеме, мы должны проанализировать каждый элемент схемы и выразить его в виде логической функции.

1) Начнем с элемента "1" входа, который не имеет предыдущего элемента и всегда имеет значение 1. Выразим его в виде логической функции:

x1 = 1

2) Далее, у нас есть элемент "И" с двумя входами: x1 и x2. Зная, что "И" возвращает 1 только тогда, когда оба его входа равны 1, мы можем выразить его в виде логической функции:

y1 = x1 * x2

3) Перейдем к элементу "ИЛИ" с двумя входами: y1 и x3. Зная, что "ИЛИ" возвращает 1 тогда, когда хотя бы один из его входов равен 1, мы можем выразить его в виде логической функции:

y2 = y1 + x3

4) И, наконец, у нас есть элемент "НЕ" с одним входом: x4. Он инвертирует значение своего входа, то есть, если x4 = 0, то выход будет равен 1, и наоборот:

y3 = x4

Теперь у нас есть логическое выражение, соответствующее данной схеме:

y3 = x4
y2 = y1 + x3
y1 = x1 * x2

Теперь, чтобы вычислить значение выражения для каждого случая:

А) x1 = x2 = 1, x3 = x4 = 0:
Подставляем значения в логическое выражение:
y3 = 0
y2 = y1 + 0 = 1
y1 = 1
Итак, значение выражения для данного случая будет y3 = 0, y2 = 1, y1 = 1.

Б) x4 = 1, и любые значения x1, x2, x3:
Подставляем значения в логическое выражение:
y3 = 1
y2 = y1 + x3
y1 = x1 * x2
Здесь y3 всегда будет равно 1, а y2 и y1 будут зависеть от значений x1, x2 и x3.

В) x1 = 0, x4 = 0, и любые значения x2, x3:
Подставляем значения в логическое выражение:
y3 = 0
y2 = y1 + x3
y1 = x1 * x2 = 0
Здесь y3 всегда будет равно 0, а y2 и y1 будут зависеть от значений x2 и x3.

Надеюсь, это помогло вам понять задачу и решить ее. Если у вас есть еще вопросы, пожалуйста, не стесняйтесь задавать.