Актуальной проблемой является рассадка зрителей в зрительном зале театра, кинотеатра, концертного зала и т.д. с соблюдением дистанции между занятыми местами. При этом желательно посадить в зале как можно больше зрителей, соблюдая минимальную требуемую дистанцию между местами. Зрительный зал представляет собой прямоугольник размером N × M, состоящий из единичных квадратов — мест. Расстоянием между местами будем считать сумму расстояний между ними по горизонтали и по вертикали. Расстояние между местами по горизонтали и по вертикали — это модуль разности их координат, считая, что расстояние между двумя соседними местами по горизонтали и по вертикали равно 1.

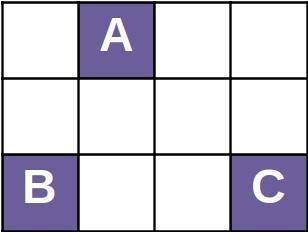
Например, на рисунке ниже изображён зрительный зал размером 3 × 4, в котором зрители сидят на трёх местах A, B и C.

Расстояние между местами A и B равно 3 (2 по вертикали плюс 1 по горизонтали), расстояние между местами B и C равно 3 (0 по вертикали плюс 3 по горизонтали), расстояние между местами A и C равно 4 (2 по вертикали плюс 2 по горизонтали).

Вам даны размеры зрительного зала N × M и минимальное расстояние между зрителями d. Вам необходимо разместить как можно больше зрителей в зале размером N × M так, чтобы расстояние между любыми двумя занятыми местами было не меньше d.

ответ нужно записать в виде N строк, каждая строка содержит M символов, равных 0 или 1. 0 обозначает свободное место, 1 обозначает занятое место.

Например, в зале размером 3 × 4 можно разместить максимум 3 человек на расстоянии не меньше 3. Пример такого размещения изображён на рисунке выше, а ответ в этом случае записывается так.

0100
0000
1001

Вам нужно дать ответ на несколько вариантов задания: 3-1, 3-2, 3-3, 3-4. На каждое задание ответ сдаётся на отдельной странице.

В задании 3-1 N = 3, M = 5, d = 2. В ответе должно быть 3 строки по 5 символов в каждой.

aksu4    3   13.12.2020 12:06    46