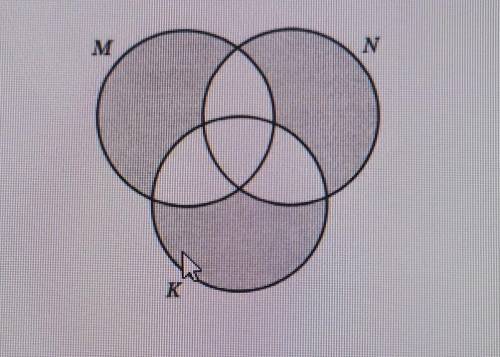
4. Выразите через базовые множества М, N, К закрашенную
область:​

Для выражения закрашенной области через базовые множества М, N, К, мы можем воспользоваться операциями над множествами - пересечения, объединения и разности.

Давайте разберемся шаг за шагом:

1. Обозначим закрашенную область как A.
2. Заметим, что A состоит из двух частей: верхнего и нижнего треугольников.
3. Верхний треугольник:
Он содержит левую сторону и нижнюю сторону, но не содержит правую сторону.
Таким образом, верхний треугольник можно выразить как (К ∩ М) ∪ (К ∩ N').

4. Нижний треугольник:
Он содержит правую сторону и нижнюю сторону, но не содержит левую сторону.
Таким образом, нижний треугольник можно выразить как (К' ∩ M) ∪ (К' ∩ N).

5. Общая закрашенная область A будет состоять из объединения верхнего и нижнего треугольников:
A = ((К ∩ М) ∪ (К ∩ N')) ∪ ((К' ∩ M) ∪ (К' ∩ N)).

Таким образом, закрашенная область выражается через базовые множества М, N, К следующим образом:

A = ((К ∩ М) ∪ (К ∩ N')) ∪ ((К' ∩ M) ∪ (К' ∩ N)).

Это детальное объяснение поможет школьнику понять, как выразить закрашенную область через базовые множества и как оперировать с пересечениями, объединениями и разностями множеств для получения итогового результата.