Знайти кути трикутника abc вершини якого є точки a(1; 3; 0) b(-2; 4; 2) c(3; 1; 0)

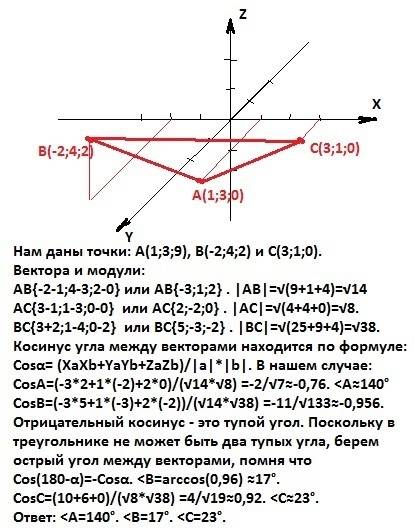
Нам даны точки: А(1;3;9), В(-2;4;2) и С(3;1;0).Вектора и модули:АВ{-2-1;4-3;2-0} или AB{-3;1;2} . |AB|=√(9+1+4)=√14AC{3-1;1-3;0-0}  или AC{2;-2;0} . |AC|=√(4+4+0)=√8.BC{3+2;1-4;0-2}  или BC{5;-3;-2} . |BC|=√(25+9+4)=√38.Косинус угла между векторами находится по формуле:Cosα= (XaXb+YaYb+ZaZb)/|a|*|b|. В нашем случае:CosA=(-3*2+1*(-2)+2*0)/(√14*√8) =-2/√7≈-0,76. <A≈140°CosB=(-3*5+1*(-3)+2*(-2))/(√14*√38) =-11/√133≈-0,956.Отрицательный косинус - это тупой угол. Поскольку в треугольнике не может быть два тупых угла, берем острый угол между векторами, помня что Cos(180-α)=-Cosα. <B=arccos(0,96) ≈17°.CosC=(10+6+0)/(√8*√38) =4/√19≈0,92. <C≈23°.ответ: <A=140°. <B=17°. <C=23°.