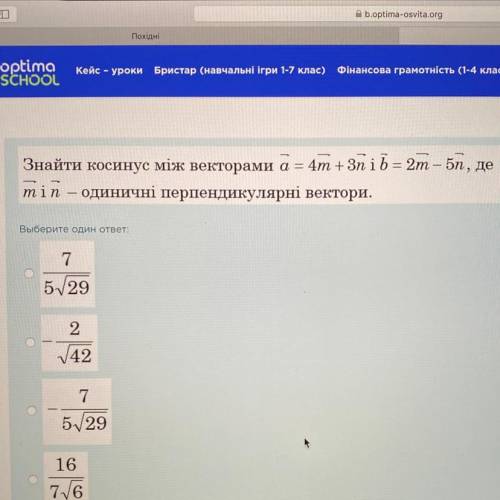
Знайти косинус між векторами а = 4m+ 3n i b = 2m– 5n, де m і n— одиничні перпендикулярні вектори.

Так как векторы m и n единичны и перпендикулярны, то  можно выразить в координатах векторы a и b, приняв вектор m по оси Ох, вектор n по оси Оу:

a = (4; 3), b = (2; -5).

Находим их модули.

|a| = √(4² + 3²) = √25 = 5,

|b| = √(2² + (-5)²) = √29.

Теперь находим косинус угла между ними.

cos (a_b) = (4*2 + 3*(-5))/(5*√29) = -7/(5√29).

ответ: cos (a_b) =  -7/(5√29).